Höchstgeschwindigkeit abgeregelt

Allzu oft liest man ja, dass die Höchstgeschwindigkeit bei 250km/h abgeregelt ist. Schade, denn man hat ja ein Auto mit 300PS vor sich und würde gern mal richtig los machen. Auch Chiptuner bieten den Service der Entdrosselung an. Wie schnell könnte denn das Auto wenn es frei gelassen wird?

300km/h, 350km/h? Hier ein kurzer Einblick in das Vermögen Höchstgeschwindigkeiten zu fahren…

Fahrdynamik: Fahrwiderstände

Zuerst einmal ist es natürlich wichtig zu wissen, welche Faktoren für die erreichbare Höchstgeschwindigkeit verantwortlich sind. In aller erster Reihe sind die Motorleistung und der Luftwiderstand zu nennen. Alle anderen Widerstände sind bei sehr hohen Geschwindigkeiten vergleichsweise gering.

Motorleistung

$P_e=M_d \cdot 2 \cdot \pi \cdot n$

wobei P=Motorleistung [kW], M=Drehmoment, n=Motordrehzahl [1/s]

Luftwiderstand

$F_\text{luft}=\cfrac{\rho}{2}\cdot c_w \cdot A \cdot v^2$

wobei F=Widerstand [N], ρ=Luftdichte [kg/m³], cw=Luftwiderstandsbeiwert, A=Stirnfläche, v=Fahrgeschwindigkeit

Rollwiderstand

$F_\text{roll} = \left( f_\text{r0} + f_\text{r1} \cdot \cfrac{v}{100} + f_\text{r4} \cdot \left( \cfrac{v}{100} \right)^2 \right) \cdot m \cdot g \cdot \cos \alpha$

wobei F=Widerstand [N], fr=Rollwiderstandsbeiwerte, m=Fahrzeugmasse, g=Erdschwerebeschleunigung, α=Steigungswinkel. Da die Rollwiderstandskoeffizienten sowieso nicht exakt bekannt sind, wird zur Vereinfachung f=0.015 angenommen und die Gleichung vereinfacht sich.

Steigungswiderstand

$F_\text{steig}=m \cdot g \cdot \sin \alpha$

wobei F=Widerstand [N], m=Fahrzeugmasse, g=Erdschwerebeschleunigung, α=Steigungswinkel

Beschleunigungswiderstand

$F_a=m \cdot a \cdot \left( 1+ \cfrac{\sum \theta}{r_\text{dyn} ^2 \cdot m} \right)$

wobei F=Widerstand [N], m=Fahrzeugmasse, a=Fahrzeuglängsbeschleunigung, θ=Massenträgheitsmoment, r=Reifenhalbmesser. Der Beschleunigungswiderstand spielt im Prinzip nur in den ersten Gängen eine Rolle. Im Bereich der Höchstgeschwindigkeit ist die Beschleunigung so gering, dass dieser Widerstand vernachlässigt werden kann.

Nimmt man jetzt an, man fährt mit einem Audi S6 auf völlig ebener Autobahn, es herrscht kein Gegen- oder Mitwind und auch keine Steigung, so spielen letztendlich für die erreichbare Höchstgeschwindigkeit nur die Radleistung und der Luftwiderstand eine Rolle.

Daten Audi S6 C6 Avant mit V10 FSI MJ2007

(Quelle: Audi.de Prospekt zum Fahrzeug)

$A=2.26m^2 \\ c_w=0.34 \\ m=1970kg$

Nimmt man dazu den Rollreibungskoeffizienten f=0.015 und die Luftdichte mit 1.2kg/m³ an, so ergibt sich folgender Fahrwiderstand:

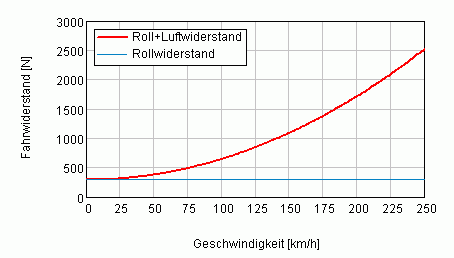
Man sieht also, bei hohen Geschwindigkeiten hat der Luftwiderstand einen erheblichen Einfluss auf die erreichbare Höchstgeschwindigkeit (Cayenne, Touareg, etc. lässt grüßen!)

Die nötige Leistung zum Erreichen der jeweiligen Geschwindigkeit ist mit

$P=\sum \limits_{i} F_i \cdot v$

definiert.

Zieht man für die Berechnung nur den Roll- und Luftwiderstand in Betracht, so ist die nötige Radleistung zum Erreichen einer gewünschten Höchstgeschwindigkeit nach

$P_\text{rad}= \cfrac{\rho}{2}\cdot c_w \cdot A \cdot v^3 + f_r \cdot m \cdot g \cdot v$

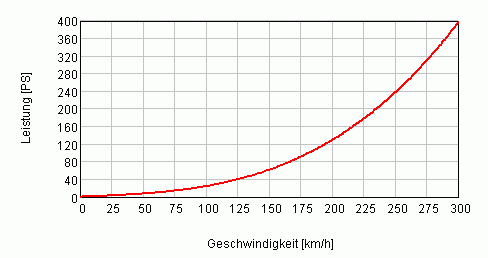
Als Beispiel die Größengleichung für 250km/h für den Audi S6 C6 Avant (V10 FSI, MJ: 2007) mit der nötigen Leistung in PS:

$P_\text{rad} = \left[ \cfrac{1.2}{2} \cdot 0.34 \cdot 2.26 \cdot \left(\cfrac{250}{3.6}\right)^3 + 0.015 \cdot 1970 \cdot 9.81 \cdot \cfrac{250}{3.6} \right] \cdot \cfrac{1.36}{1000} = 237 \text{PS}$

Durch die 435PS, die der V10 Motor leistet, kann man in diesem Fall wirklich von “abgeregelt” sprechen.

Höchstgeschwindigkeit

[Edit: Aus dem Kommentar von Jan, Danke!]

$v_\text{max}\approx 100 \cdot \sqrt[3]{\cfrac{P}{k \cdot c_w \cdot A}}$

Ist eine umgestellte Größengleichung mit P…Motorleitung (KW) und k…Korrekturfaktor (16-18) aus “Aerodynamik des Automobils“, ATZ/MTZ-Fachbuch

Der Audi S6 C6 Avant (V10 FSI, MJ: 2007) würde demnach eine Geschwindigkeit von

$v_\text{max}\approx 100 \cdot \sqrt[3]{\frac{320}{16 \cdot 0{,}34 \cdot 2{,}26}}=300km/h$

erreichen.

Achtung – Realität!

Die hier getätigten Berechnungen sind absolut theoretischer Natur! Die in den Prospekten angegebene Leistung der Fahrzeuge ist die auf dem (konditionierten) Prüfstand ermittelte Motorleistung. Die Leistung die an den Rädern ankommt ist um ein erhebliches Maß geringer als die Motorleistung. Außerdem weiß man im realen Einsatz oft nicht die exakte Dichte der Luft, den Rollreibungswiderstand oder die Wirkungsgrade aller am Vortrieb beteiligten Bauteile. Des weiteren ist die Getriebeauslegung eventuell nicht so vorgenommen worden das die Höchstgeschwindigkeit auch bei der höchten Leistung erreicht werden kann. Dort ist eine detaillierte Betrachtung des Zugkraftdiagramms mit der darin enthaltenen Getriebeabstufungen nötig.

Wo wir gerade bei Höchstgeschwindigkeit sind:

Verbrauch

Der Streckenverbrauch (also l/100km) eines Fahrzeugs ist mit folgender Größengleichung zu berechnen

$b_s = \cfrac{b_e \cdot P_e}{\eta_T \cdot v \cdot \rho_K \cdot 10}$

definiert. Darin sind be=effektive spezifische Verbrauch [g/kWh], η=Wirkungsgrad, v=Fahrgeschwindigkeit [km/h], ρ=Kraftstoffdichte [g/cm³], P=Leistung [kW].

Das be-Kennfeld (Umgangssprachlich: Muscheldiagramm) eines Motors ist wohl das best behütetste Geheimnis eines jeden Automobilherstellers. Daher liegt mir auch keines des V10 FSI vor. Nimmt man aber mal an, dass der be=300g/kWh bei dieser Leistung ist, dann beläuft sich der Streckenkraftstoffverbrauch auf

$b_s = \cfrac{300 \cdot 174.5}{0.8 \cdot 250 \cdot 0.72 \cdot 10} = 36 \text{ l/100km}$

Wer mal selbst probieren möchte, findet eine Excel Tabelle mit allen Formeln:

Download

Titelbild unter CC-BY-SA2.0 Lizenz von flickr.com von Paulo Keller

3 Comments

Jan sagt:

8. August 2012 um 09:05 Uhr

Die zur Überwindung des Luftwiderstandes nötige Antriebsleitung nimmt mit der dritten Potenz der Fahrgeschwindigkeit zu. Näherungsweise kann die Höchstgeschwindigkeit (in km/h) daher wie folgt bestimmt werden:

vmax = 100 * 3.Wurzel aus (P/(k * cW * A))

mit P…Motorleitung (KW) und k…Korrekturfaktor (16-18)

aus “Aerodynamik des Automobils”, ATZ/MTZ-Fachbuch

Antworten
1. Daniel sagt:
  
  15. April 2021 um 08:33 Uhr
  
  Woher stammt die Formel zur Beschreibung des Rollwiderstandes?
  
  Antworten
Znarf sagt:

17. November 2017 um 13:38 Uhr

„wo steht das genau mit der 3. Potenz in Aerodynamik des Automobils“, ATZ/MTZ-Fachbuch?

https://books.google.at/books?id=LtSIBwAAQBAJ&pg=PA157&lpg=PA157&dq=%E2%80%9EAerodynamik+des+Automobils%E2%80%9C+luftwiderstand&source=bl&ots=jVEX1osdIz&sig=tGlUe2P8OZJNLLacI8L3YAwgz00&hl=de&sa=X&ved=0ahUKEwjygozCzsXXAhUPY1AKHR91AQoQ6AEIaDAP#v=onepage&q=%E2%80%9EAerodynamik%20des%20Automobils%E2%80%9C%20luftwiderstand&f=false

Antworten

Motorblog

Höchstgeschwindigkeit abgeregelt