Man kann es ja nicht leugnen, so ein Starr-Rahmen sieht einfach klasse aus. Das findet der Prüfer beim DEKRA oder TÜV auch, aber er sieht die Gefahren. Welche das sind, wird bei folgender einfachen Berechnung deutlich.
Überfahren einer Kante
Wären alle Straßen so schön eben, wie man davon träumt, gäbe es keinen Grund zur Sorge. Leider sehen sogar Autobahnen oder Landstraßen eher mittelmäßig bis schlecht aus, sodass die Feder-Dämpfer-Elemente am Motorrad einiges zu tun bekommen. Deren Aufgabe ist es nämlich, den Reifen möglichst stark und dauerhaft auf den Boden zu pressen ohne dabei den Fahrer von der Maschine zu werfen.
Zur mathematischen Beschreibung und Animation des Sachverhalts wird ein Feder-Masse-Dämpfer Element genommen, welches bei einem Motorrad genau die Hälfte des Fahrzeugs darstellt. Nickbewegungen des Motorrades werden also nicht durch die Berechnungen erfasst. Die Werte für Federkonstanten, Dämpfungskonstanten und Massen sind frei gewählt. Wer genauere Angaben hat, bitte in den Kommentare vermerken.
Zu beachten ist vor allem, dass das Rad (grün) der Bewegung der Straße (grau) folgt. Dies ist wichtig, damit es jederzeit zur notwendigen Kraftübertragung kommt. Die ruhige Bewegung des Fahrers (blau) ist ein Komfortmerkmal, welches ebenfalls wichtig ist.
Starr-Rahmen heißt: Kaum Federung und kaum Dämpfung
Ein Starr-Rahmen hat nun genau diese Federung und Dämpfung nicht mehr. Genau genommen federt der Stahl zwar noch etwas, dies ist aber für Bodenwellen nicht mehr sehr hilfreich. Denn jedes der Elemente ist für einen eigenen Frequenzbereich zuständig. Der Reifen federt hohe Frequenzen ab, ein Dämpfer die Mittleren. Eine Bodenwelle kann zu den mittleren Frequenzen gezählt werden. Man nimmt sie nicht mehr als ‘Brummen’ wahr, sondern schon als ‘Bewegung’.
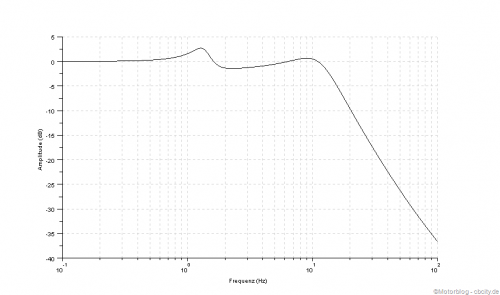
Amplitudenverstärkung zwischen Reifen und Fahrbahn für Schwingungsanregungen zwischen 0Hz…100Hz. Steigt diese Kurve über 0db, so ist eine Dämpfung notwendig, da es sonst zum Aufschaukeln der Bewegung kommt. In diesem Beispiel ist der Bereich um 1.5Hz (die Eigenfrequenz der Radschwingung), welche durch den Stoßdämpfer unbedingt abgedeckt werden muss.
Um die nicht mehr vorhandene Federung und schlechte Dämpfung zu simulieren, wird die Federsteifigkeit auf 2000kN/m erhöht, die Dämpfung auf 10Ns/m reduziert. Das Ergebnis ist folgendes:
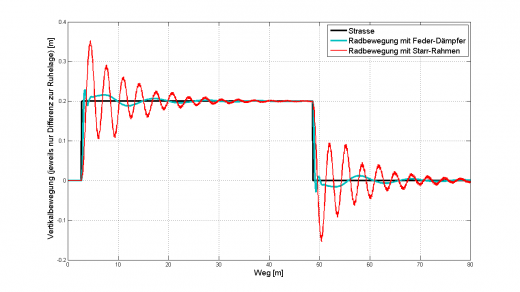
Es ist zu sehen, dass das Überfahren einer 20cm hohen Kante das gesamte Gefährt zum schwingen bringt. Das Rad hebt von der Straße ab, die Fahrt wird auf einer Geraden sehr unruhig. In einer Kurve kann das den Tod bedeuten, sollte das Hinterrad keine Querkräfte mehr übertragen können, weil es vom Boden abhebt.
Vergleich der Schwingung mit Feder-Dämpfer-Element und Starr-Rahmen
Matlab Code zur Berechnung der Schwingung
% check ob Toolbox installiert ist für Zustandsraummodell
if exist('ss')==2
disp('System Control Toolbox ist installiert')
else
disp('System Control Toolbox wird benötigt')
return
end
clc; clear all;
% Systemparameter
m1 = 20; %Radmasse /kg
m2 = 2000/4; %Aufbaumasse /kg
m3 = 80/4; %Fahrermasse /kg
c1 = 100000; %Federsteifigkeit Rad /N/m
c2 = 200; %Federsteifigkeit Fahrwerk /N/m
c3 = 10000; %Federsteifigkeit Sitz /N/m
k2 = 1400; %Dämpfung Stoßdämpfer /Ns/m
k3 = 300; %Dämpfung Sitz /Ns/m
tend=10; %Simulationsdauer
%Systemmatrix
A = [ 0 1 0 0 0 0;
-(c2+c1)/m1 -k2/m1 c2/m1 k2/m1 0 0;
0 0 0 1 0 0;
c2/m2 k2/m2 -(c3+c2)/m2 -(k3+k2)/m2 c3/m2 k3/m2;
0 0 0 0 0 1;
0 0 c3/m3 k3/m3 -c3/m3 -k3/m3];
%Steuermatrix
B = [0 c1/m1 0 0 0 0]';
%Beobachtungsmatrix
C = [1 0 0 0 0 0]; % Radbewegung wird beobachtet
%Durchgriffsmatrix
D = [0];
%Zeitbasis
t=0:0.001:tend;
%Eigenfrequenzen
fRad =round(100*sqrt((c1+c2)/m1)/(2*pi))/100
fAufbau =round(100*sqrt(c2/m2)/(2*pi))/100
fFahrer =round(100*sqrt(c3/m3)/(2*pi))/100
% Straße
f=fRad; %Anregungsfrequenz
%h=cos(f*t*2*pi)*0.2-0.2; %Sinusanregung
h=[zeros(500,1); 0.1*ones(length(t)-500,1)]'; %Kante
%h=rand(1,length(t))*0.2; %stochastische Anregung
% Berechnung
system = ss(A,B,C,D); %Definition des Zustandsraummodells
[y,t,x]=lsim(system,h,t); %Simulation
v = 50 / 3.6; %Geschwindigkeit
s = v.*t;
Radhub = x(:,1);
Aufbauhub = x(:,3);
Fahrerhub = x(:,5);
kontaktmass = norm(h'-Radhub,2)
plot(s, [h', Radhub, Aufbauhub],'LineWidth',3);
set(gcf,'Position',[100 100 1280 720],'Paperpositionmode','Auto')
grid on
legend('Strasse','Rad','Aufbau');
ylim([-0.1 1])
xlabel('Weg [m]');
ylabel('Vertikalbewegung [m]');
title({['Aufbaubewegung beim Überfahren einer Kante mit ' num2str(v*3.6) 'km/h'];...
['Federsteifigkeit c=' num2str(c2/1000) 'kN/m']},'Fontsize',14);
text(10, 0.5,['Kontaktmaß Rad-Straße (L2-Norm) = '...
num2str(kontaktmass) ' (niedriger ist besser)'],...
'Fontsize',12)
print(['Federsteifigkeit-' num2str(c2/1000) 'kN.png'],'-dpng','-r300')








5 Comments
Es ist zu sehen, dass das Überfahren einer 20cm hohen Kante das gesamte Gefährt zum schwingen bringt.
Eine 20 CM !! hohe Kante ???? Da hilft auch Federung nix mehr :-)
Hallo Blechgott,
die 20cm sind ein durchaus realistisches Maß (vgl.: http://www.khs-flensburg.de/documents/SCH-WenndieFahrtimSchlaglochendet.pdf) und werden von Gerichten etc. als kritische Tiefe für Schlaglöcher angesehen.
Wenn ich statt “Kante” lieber “Schlagloch” schreiben soll, kann ich das gern tun.
Hi,
Sehr schön veranschaulicht und prinzipiell ist die Aufgaben auch richtig.
Allerdings ist eine Radeigenfrequenz des Rades mit 1.5Hz viel zu klein. Das sollten eher so 13Hz sein.
Auch dass beim Reifen keine Dämpfung angenommen wird, finde ich etwas fragwürdig…
Auch wenn die Sache hier schon älter ist, will ich mal meinen Senf dazu geben. Schöne Animation und sicher auch alles richtig gerechnet, aber als Starrrahmenfahrer (mit langer Springergabel ohne Dämpfung) kann ich nur sagen, daß da Theorie und Praxis WEIT auseinander liegen. Bodenwellen, besonders in Kurven, bringen schon Unruhe ins Fahrwerk, aber wenn man das weiß, kann man damit leben. Ein 20 cm tiefes Schlagloch halte ich schon für sehr extrem, aber je nach Größe wird das in der Praxis weitestgehend “überflogen”, bei langsamer Geschwindigkeit könnte (und sollte) man ausweichen, zumindest, wenn man seine Felgen mag. Starrahmen fahren schult in dieser Hinsicht auch das Auge, wer ein paar Mal einen Tritt ins Kreuz bekommen hat, wird aufmerksamer. Historisch gesehen hätte es ja dann früher massenhaft Tote geben müssen, da fuhren ja fast ausschließlich Starrrahmendurch die Gegend, ok, da war der Sattel gefedert, aber trotzdem…..
Tja.. viel Ahnung von nichts !