Interpolation hat fast jeder schon einmal gehört. Man benötigt zu bestehenden Messwerten eine feiner Auflösung und bestimmt Zwischenstellen linear, polynomisch oder mittels Spline. Im nachfolgenden Bild ist eine lineare Interpolation (orange) zu bestehenden Messwerten (blau) zu sehen.
Orangener Wert ist linear interpoliert zu den bestehenden blauen Werten
Es gibt allerdings auch noch wesentlich ausgeklügeltere Verfahren der Interpolation, mit dessen Hilfe man erstaunliche Ergebnisse erzielen kann. Im Folgenden soll beispielhaft die Interpolation einer harmonischen Schwingung mit Matlab erfolgen.
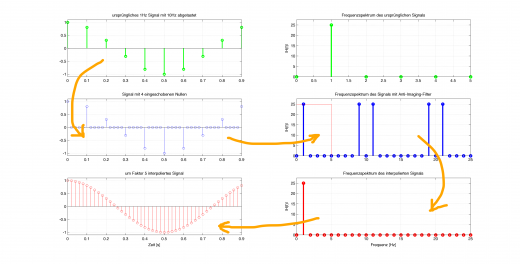
Ursprüngliches Signal: 1Hz Schwingung
Das ursprüngliche Signal soll beispielsweise eine Schwingung mit 1Hz sein, welches mit nur 10Hz abgetastet (digitalisiert) wurde.
%% Signal generieren fa=10; %Abtastrate in Hz t=0:1/fa:(1-1/fa); %Zeitvektor f=1; %Signalfrequenz in Hz y=cos(2*pi*f*t); %Signal
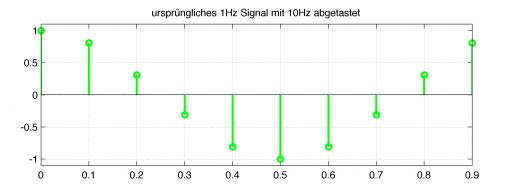
Zwischen diesen Datenpunkten könnte man jetzt linear oder polynomisch interpolieren und damit die Auflösung erhöhen. Doch gerade bei periodischen Signalen (hier: Cosinus-Schwingung) gibt es eine sehr viel bessere Methode! Die Abtastratenerhöhung durch Interpolation mittels Anti-Imaging-Filterung.
Dazu muss das Signal in den Frequenzbereich transformiert werden. Dies geschieht am effektivsten mit der Fast-Fourier-Transformation.
Y = fft(y);
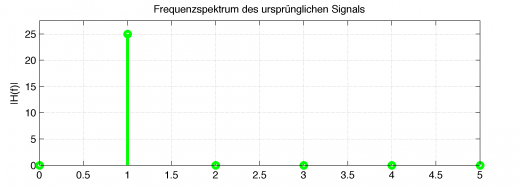
Im Frequenzbereich stellt sich die harmonische 1Hz-Schwingung mit einem Peak bei 1Hz dar. Jetzt kommt der Trick!
Einfügen von Nullen in den Signalverlauf
Sagen wir, man möchte die Abtastrate um den Faktor L=5 erhöhen. Also von 10Hz auf 50Hz soll das Signal interpoliert werden.
%% Interpolationsfaktor L=5;
Der erste Schritt ist folgender: Man fügt einfach L-1=4 Nullen zwischen den ursprünglichen Signalwerten ein.
%% 1. Nullen in Zeitsignal einfügen
y_L = zeros(L,length(y));
nullen = zeros(1,L-1);
for i=1:1:length(y)
y_L(:,i) = [y(i) nullen];
end
% Umsortieren um wieder einen Datenvektor zu erzeugen
y_L=reshape(y_L,[],1);
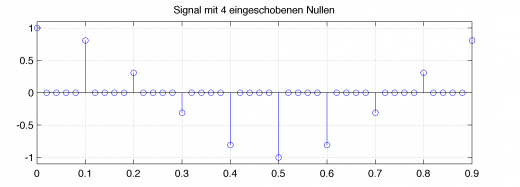
Diese Nullen stehen ja nun schon an den richtigen Stellen, allerdings fehlt noch der korrekte Wert um das Signal optimal zu ergänzen. Die Lösung ist über das Frequenzspektrum zu bekommen.
Frequenzspektrum des mit Nullen versehenen Signals
Y_L = fft(y_L);
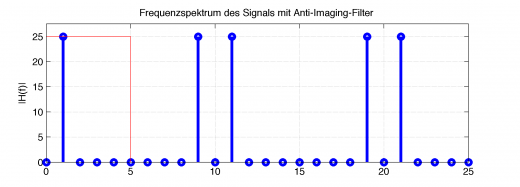
Frequenzspektrum (blau) des mit Nullen versehenen Signals und entsprechendem Anti-Imaging-Tiefpassfilter (rot)
Hier ist nun folgendes Interessant: Durch die eingefügten Nullen ist natürlich die Abtastrate des Signals “erhöht” worden. Dadurch kann im Frequenzbereich auch bis zu einem höheren Frequenz das Spektrum berechnet werden. Das ursprüngliche Signal konnte bis zur Hälfte der Abtastrate (Beachtung der Nyquist-Frequenz) berechnet werden. Das waren also 5Hz. Das um den Faktor L=5 höher abgetastete Signal kann auch mit 5facher Grenzfrequenz (also 25Hz) berechnet werden. Es entstehen zusätzliche Spektren, die so genannten “Image-Spektren”, im Frequenzbereich. Wieso, warum, weshalb?
Anti-Imaging-Filter
Nun wird ein “Anti-Imaging-Filter”, welcher ein Tiefpass mit der Grenzfrequenz der ursprünglichen halben Abtastrate ist, auf das Spektrum angewendet. Dieser löscht alle Werte oberhalb der halben Abtastrate des ursprünglichen Signals (also oberhalb 5Hz).
%% 3. Löschen der Imagespektren Y_L(fa/2:length(Y_L))=0;
Das neue Frequenzspektrum sieht aus wie das Alte, allerdings mit einer Grenzfrequenz von 25Hz.
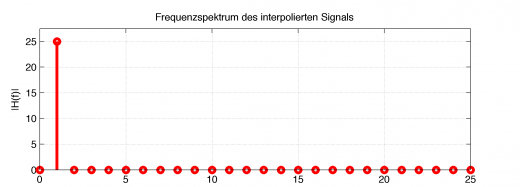
Dieses Frequenzspektrum widerum ist die Abbildung eines mit dem Faktor 5 ideal interpolierten Signals.
Inverse FFT erzeugt optimal interpoliertes Signal
%% inverse FFT y_up = L.*ifft(Y_L,'symmetric');
Das Signal muss noch mit dem Interpolationsfaktor Multipliziert werden, damit die Signalleistung wieder identisch dem Eingangssignal ist.
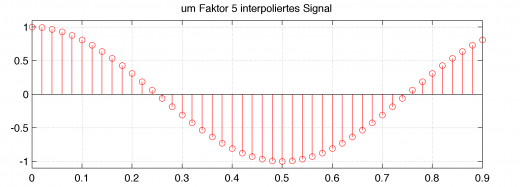
Ergebnis der inversen FFT des veränderten Frequenzspektrums nach Anti-Imaging-Filter: perfekte Interpolation
Als Ergebnis erhält man ein perfekt interpoliertes Signal.
Zusammenfassung zum Ablauf