Die Grundlage von enorm vielen Bildverarbeitungsalgorithmen ist die Kantenerkennung. Das bedeutet, dass in einem Bild die Umrisse eines Objekts herauszufinden sind oder markante Linien gefunden werden.
Doch wie funktioniert solch ein Algorithmus im Detail?
Was ist ein Bild für den Computer?
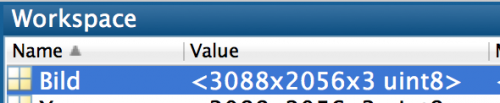
Dimension eines 6MP Fotos
Fängt man mit einer Linse eine Situation ein, so speichert der Chip in der Kamera in Abhängigkeit des Orts auf dem Chip die Farbwerte ab. Fast alle Farben können zum Beispiel mit rot, grün und blau ziemlich gut zusammengesetzt werden. Die codierung der Farbwerte ist mit 8bit festgelegt, was die diskreten Werte von 0…255 ermöglicht. Hat ein Chip einer Digitalkamera ca. 6 MegaPixel, so hat ein Foto, welches mit der Kamera geschossen wurde, eine Dimension von 3088x2056x3. Höhe und Breite in Pixel sind jedem geläufig, doch interessant wird es bei dem x3. Dies ist der RGB Vektor, welcher den Anteil der Farben beinhaltet.

links: Detailvergrößerung des Fotos mit markiertem Ausschnitt (blauer Rahmen) für pixelgenaue Darstellung des Farbcodes rechts.
An der Abbildung oberhalb ist auf der rechten Seite zu erkennen, dass für jedes Pixel die Farbwerte für R (=rot), G (=grün) und B (=blau) abgespeichert sind. Im unteren Bereich, welcher eher rot ist, sind die Anteile von rot hoch. Ein perfekt weißes Pixel hätte den Farbcode
\(X_\text{weiss}=[255; 255; 255]\)Ein perfekt schwarzes Pixel die Farbcodierung
\(X_\text{scwar}=[0; 0; 0]\)Grauwert
Viele Bildverarbeitungsalgorithmen funktionieren nur mit Grau- statt Farbwerten. Deshalb wird in vielen Fällen der Farbvektor in eine einzige Information, nämlich den Grauwert umgerechnet. Dies kann beispielsweise mit folgender Formel geschehen:
\(\text{Grau}=0{,}2989 \cdot R + 0{,}5870 \cdot G + 0{,}1140 \cdot B\)Das Resultat der Grauwertberechnung ist, dass das Bild nur noch die Dimension 3088x2056x1 hat.

Der Matlab Code zum Berechnen dieses Ablaufs ist:
Bild = imread('foto.jpg');
imshow(Bild);
Bildgray = rgb2gray(Bild);
Die Frage ist nun, wie erkennt man auf einem Foto Kanten?
Kantenerkennung ist Mathematik
Traurig aber wahr, es ist keine Hexerei sondern Mathematik. Der Mathelehrer hat sich höchstwahrscheinlich schwer getan ein Anwendungsbeispiel zu finden, aber hier ist es. Die diskrete Faltung (engl. Convolution) ist der mathematische Hintergrund zur Kantenerkennung. Was ist Faltung?
Bildlich gesprochen wird eine Funktion mit einer anderen gefaltet, wenn die Funktion gespiegelt über die andere geschoben wird. Eine schöne Animation ist in diesem Video ab 0:40min zu sehen:
Wer mal selbst etwas herumprobieren möchte, der kann sich gern folgende Excel Tabelle runterladen: [Download Diskrete Faltung Convolution mit Excel]
Die Frage ist, was das jetzt mit Kantenerkennung zu tun hat.
Grauwertverlauf
Geht man ein Bild Pixel für Pixel durch, so stellt der Grauwert eine diskrete Funktion dar. Für das Graubild, welches oben angegeben ist, wäre ein beispielhafter Grauwertverlauf für die 1688 Spalte und Pixel Nummer 1386 bis 1386.
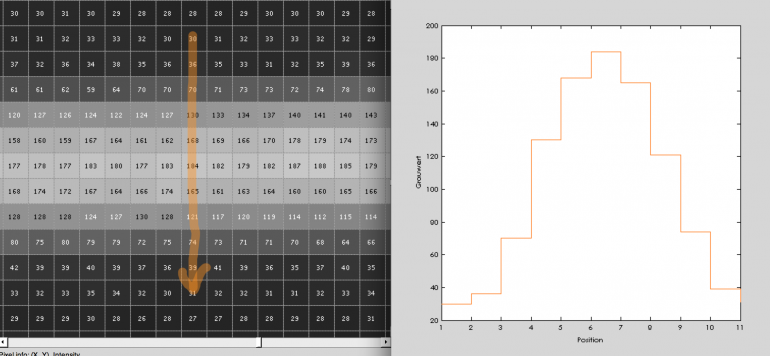
Nun hätte man schon die erste Funktion für die Faltung. Der Zauber an der Sache kommt in’s Spiel, wenn man die zweite Funktion wählt, mit welcher gefaltet werden soll. Diese wird in der Bildverarbeitung auch Kernel oder Operator genannt, denn diese ist nun frei wählbar, je nachdem, was man erreichen möchte.
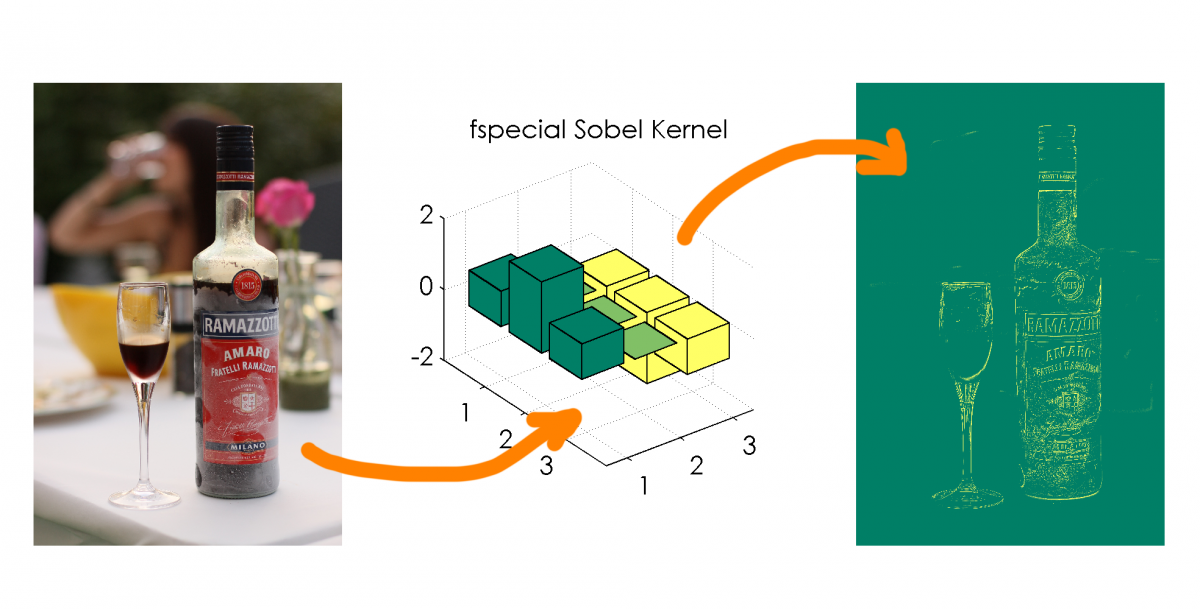
Sobel Kern als Verstärkung für Grauwertsprünge
Im Falle der Kantenerkennung kann z.B. ein Sobel-Kernel genutzt werden. Da ein Bild ja nicht 1-Dimensional, sondern 2 Dimensional abgebildet wird, muss der Sobel-Operator auch 2D sein. Er ist eine Matrix, welche nachfolgend definiert ist:
\(h=\begin{bmatrix}1 & 2 & 1 \\
0 & 0 & 0 \\
-1 & -2 & -1
\end{bmatrix}\)
Mit Matlab erzeugt ist dieser schnell:
h = fspecial('sobel');
Wird nun dieser Sobel Operator mit dem Grauwertbild gefaltet, so passiert etwas erstaunliches: Eine Faltung im Zeitbereich ist eine Multiplikation im Frequenzbereich. Der Operator verstärkt durch die (vertikalen) Sprünge von 2 auf 0 auf -2 hohe Frequenzen, d.h. starke Änderungen des Grauwertes von einem zum nächsten Pixel werden in vertikaler Richtung verstärkt. Durch die moderaten Änderungen in horizontaler Richtung (1 auf 2 auf 1) wirkt der Operator in horizontaler Richtung wie eine Glättung.
Invertiert man den Sobel-Operator, so tauscht sich die Empfindlichkeit für horizontal und vertikal, d.h. es werden die horizontalen Grauwertänderungen verstärkt, was dazu führt, dass senkrechte Kanten zu sehen sind.

Sobel-Operator für eine Erkennung von starken Grauwertsprüngen in horizontaler Richtung erzeugt Verstärkung für vertikale Kanten
Die Matlab Implementierung dieses Vorgangs ist relativ simpel:
Xhorizontal=conv2(Bildgray,h'); % Berechnung der Faltung
Zu beachten die Invertierung des Sobel Operators, in Matlab mit dem ‘ realisiert.
Überlagerung von horizontaler und vertikale Verstärkung
Dies geschieht nun nach dem Satz des Pythagoras:
\(Bild=\sqrt{\text{Bild}_\text{horizontal}^2 + \text{Bild}_\text{vertikal}^2}\)In Matlab ist die Abfolge ebenso einfach:
Xhorizontal=conv2(Bildgray,h'); Xvertical=conv2(Bildgray,h); Xsm = sqrt(Xhorizontal.^2+Xvertical.^2);
Die Zusammenfassung der verstärkten Kantenwerte in horizontaler und vertikaler Richtung sind nun im Bild Xsm gespeichert, welches so aussieht:

Bild mit verstärkten Kanten als 3. Dimension
Was hier das Interessante ist: Die 3. Dimension sind nun die verstärkten Grauwertänderungen, welche ja die Kanten darstellen.
Setzt man einen Schwellwert an, so hat der Algorithmus, welcher eigentlich nur eine mathematische Faltung ist, die Kanten im Bild gefunden.
Übrigens…
Wählt man als Operator nicht den Sobel-Kernel, sondern einen anderen, beispielsweise eine Gauss-Verteilung, so werden nicht die Kanten verstärkt, sondern man erhält ein unscharfes Bild.






One Comment