Etwas provokant ist die Frage ja schon. Keines von beidem ist sicherlich die 1. Wahl. Dennoch kann man die Frage mit Hilfe einfacher Berechnungsformeln aus der Unfallrekonstruktion beantworten.
Man ist mit seinem PKW auf der Landstraße unterwegs und eine Kollision ist unvermeidlich. Welche Aufprallsituation stellt sich für mich rein rechnerisch optimaler dar (wenn man in dem Fall von optimal sprechen darf)? Wähle ich den Gegenverkehr, welcher sich mit gleicher Geschwindigkeit nähert oder den still stehenden Baum am Straßenrand?
Auf den ersten Blick scheint der ruhende Baum die bessere Wahl, da man ja nicht mit dem entgegen kommenden Verkehr kollidieren möchte. Doch da gibt es etwas zu beachten.
Die Frage lässt sich pauschal nämlich nicht beantworten. Elementar für eine Bewertung sind die Fahrzeugmassen. Es wird auch nicht davon ausgegangen, dass jemand in einer Schrecksekunde noch Fahrzeugmassen schätzt und dann eine Entscheidung trifft. Es soll vielmehr ein Denkanstoß sein.
Man definiert folgendes:
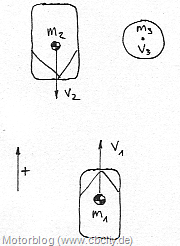
Fahrzeug 1 fährt und hat die Wahl, Kollision mit Fahrzeug 2 (entgegenkommend, gleiche Geschwindigkeit) oder Baum (stillstehend).
\(m_1=1200kg\)
\(v_1=100km/h\)
\(m_2=1200kg\)
\(v_2= – 100km/h\)
Die Geschwindigkeit des entgegenkommenden Fahrzeugs muss negativ angenommen werden, weil es in die andere Richtung fährt.
Wichtig für die Berechnung ist noch der so genannte Restitutionskoeffizient, welcher eine Aussage über die Ein- und Auslaufgeschwindigkeit des Unfalls gibt.
\(\epsilon=0 \text{ vollkommen plastischer Aufprall}\) \(\epsilon=1 \text{ vollkommen elastischer Unfall somit Fahrzeug ohne Deformationen}\)In der Realität ist der Restitutionskoeffizient bei PKW/PKW Kollisionen von der Fahrzeugart, Masse und Fahrgeschwindigkeit abhängig und liegt irgendwo zwischen 0.1 und 0.2. Es wird aber trotzdem einfach
\(\epsilon=0{,}1\)definiert.
Fall 1: Kollision mit Gegenverkehr
Ein entscheidender Faktor für die Bewertung der Unfallschwere ist die Geschwindigkeitsänderung, welcher das Fahrzeug und damit deren Insassen ausgesetzt sind. Eine hohe Geschwindigkeitsänderung durch den Unfall ist eher nachteilig. Die Geschwindigkeitsänderung kann in Anlehnung an den geraden zentrischen Stoß nachfolgend berechnet werden
$$\Delta v_1= – \frac{m_2 \cdot (1+\epsilon)}{m_1+m_2} \cdot (v_1-v_2)$$
Die Werte eingesetzt ergibt sich
$$\Delta v_1= – \frac{1200kg \cdot (1+0{,}1)}{1200kg+1200kg} \cdot (100km/h-(-100km/h))$$
$$\Delta v_1=-110km/h$$
Aua, das ist ein ganzschöner Knall. Das dürfte im überwiegenden Teil der Kollisionen die Mortalitätsrate noch oben korrigieren. Trauer.
Das Fahrzeug fährt mit 100km/h auf ein entgegenkommendes Fahrzeug auf und wird durch den Crash mit 10km/h in die andere Richtung geschleudert. Im Falle des gerade, zentrischen Stoßes kommt es zu keiner Rotation, somit ist die Geschwindigkeitsänderung für das Fahrzeug insgesamt 110km/h.
Fall 2: Kollision mit dem Baum
Das Problem an einem Baum ist, dass er relativ unbeweglich ist. Das spiegelt sich darin wider, dass die Masse des Baums nicht mit 1200kg in die Kollisionsrechnung eingeht, sondern mit “unendlicher” Masse. Das ist ein Maß dafür, dass der Baum sich “keinen Millimeter” weg bewegt, wenn man mit einem Auto gegen ihn fährt.
\(m_3= \infty kg\) \(v_3=0 km/h\)Diese Werte in die Berechnungsformel eingesetzt ergibt
$$\Delta v_1= – \frac{\infty \cdot (1+0{,}1)}{1200 kg + \infty kg} \cdot (100km/h-0km/h)$$
Zur Berechnung muss man das “unendlich” ausklammern, sodass
$$\Delta v_1= – \frac{\infty}{\infty} \cdot \frac{1{,}1}{\frac{1200kg}{\infty kg}+1}\cdot (100km/h)$$
entsteht. Der erste Term fällt weg, der Ausdruck 1200kg/”unendlich” ist “unendlich” klein, somit 0. Damit bleibt
$$\Delta v_1=-110km/h$$
Erstaunlich. Offensichtlich macht es rechnerisch überhaupt keinen Unterschied ob man gegen einen Baum ausweicht oder in den Gegenverkehr. Beides bei diesen Geschwindigkeiten höchstwahrscheinlich tötlich.
Jetzt könnte man noch Diskussionen über Kompatibilitätsprobleme zwischen Baum und PKW anstellen, oder einwenden, dass im Gegenverkehr auch noch Menschen gefährdet werden usw… Darum sollte es nicht gehen.
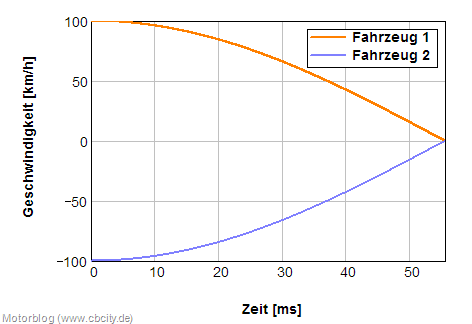
Zeitverlauf einer Kollision PKW/PKW
Um einen Eindruck dafür zu bekommen, wie die Geschwindigkeitsverläufe einer Kollision PKW/PKW sind, kann man die Bewegungsdifferentialgleichungen lösen. Dazu muss bedacht werden, dass sich die PKW Front wie eine Feder verhält, welche die Bewegungsenergie aufnimmt. Eigentlich wird die Bewegungsenergie in Verformungsenergie umgewandelt, aber für die Berechnung der zeitlichen Verläufe, kann mit einer Federsteifigkeit der Fahrzeugstrukturen gerechnet werden. Diese wird aus Frontalkollisionen gegen eine undeformierbare Barriere empirisch ermittelt. Es kann von einem Zusammenhang zwischen Fahrzeugmasse und Federsteifigkeit ausgegangen werden. Beispielhaft soll mit einem linearen Zusammenhang von
\(\kappa=800 \frac{1}{s^2}\)gerechnet werden. Das ergibt für die Fahrzeuge mit 1200kg eine Federsteifigkeit von 960kN/m.
Für die Kollision wird eine Ersatzfedersteifigkeit für beide PKW ermittelt, welche sich aus
\(c_{ers}=\frac{c_1 \cdot c_2}{c_1+c_2}\)ergibt. Der Eigenwert der Bewegungsdifferentialgleichung ist
$$\omega_2=\sqrt{c_{ers} \cdot \frac{m_1+m_2}{m_1 \cdot m_2}}$$
Damit ergibt sich die ausformulierte Bewegungsdifferentialgleichung für die Fahrzeuge zu
$$v_1(t)=\left[ \frac{m_1}{m_1+m_2} \cdot (v_1-v_2)+v_2 \right] + \frac{m_2}{m_1+m_2} \cdot (v_1-v_2) \cdot \cos(\omega_2 \cdot t)$$
$$v_2(t)=\left[ \frac{m_1}{m_1+m_2} \cdot (v_1-v_2)+v_2 \right] – \frac{m_1}{m_1+m_2} \cdot (v_1-v_2) \cdot \cos(\omega_2 \cdot t)$$
Dies ergibt folgenden Geschwindigkeits-Zeit-Verlauf für die Kollision.
Mortalitätsrate vs. Fahrzeuggewicht
Schaut man sich Unfallstatistiken an, so stellt man fest, dass die Mortalitätsrate (Sterberate) rapide sinkt, umso schwerer das Fahrzeug wird. Warum ist das so?
Berechnet man den Geschwindigkeits-Zeit-Verlauf nochmal mit anderen Fahrzeugmassen, so wird dies deutlich. Lässt man z.B. einen Audi Q7 gegen einen Smart kollidieren, so sehen die Massenverhältnisse ganz anders aus.
\(m_{Q7}=2600kg\)
\(m_{Smart}=805kg\)
Die theoretische Ersatzfedersteifigkeit und die Bewegungsgleichungen verändern sich dramatisch:
Geschwindigkeits-Zeit-Verlauf
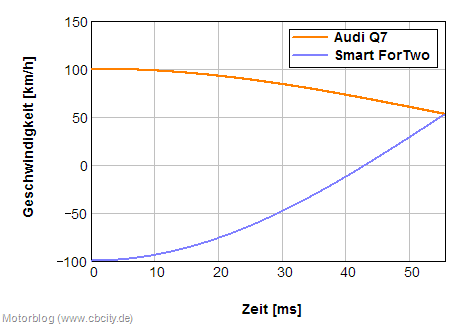
Bei dieser Kollision würde der Q7 also theoretisch noch mit über 50km/h in seine ursprüngliche Richtung weiter fahren, der Smart hätte seine Geschwindigkeit in ca.55ms um 150km/h geändert.
Beschleunigungs-Zeit-Verlauf
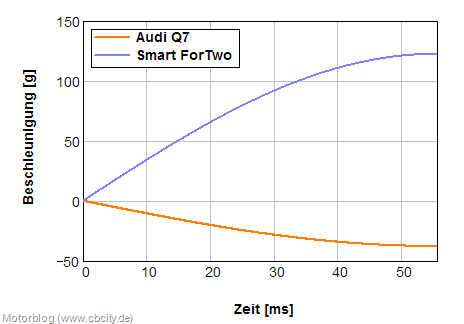
Rein theoretisch, aber schon auf dem Papier nicht schön!
Titelbild: Crashed Into A TreeVon bikesandwich unter CC-BY-NA2.0 Lizenz







One Comment