In vielen Bereichen der Ingenieurstätigkeit bilden Differentialgleichungen die realen Zusammenhänge mathematisch ab. Dabei ist eine Differentialgleichung eine Gleichung, die außer der unbekannten Funktion y(x) auch noch deren Ableitungen y’(x), y’’(x), … yn(x) enthält. Die höchste vorkommende Ableitung n wird als Ordnung der Differentialgleichung bezeichnet. Die Lösung von Differentialgleichungen sind keine konkreten Zahlen (wie bei herkömmlichen Gleichungen), sondern ebenfalls Gleichungen! Je nach Anfangsbedingungen entstehen für ein und dieselbe Differentialgleichung unterschiedliche Lösungsgleichungen. Oftmals sind Differentialgleichungen auch gar nicht symbolisch lösbar, so dass sowieso nur eine numerische Berechnung zum Ziel führt.
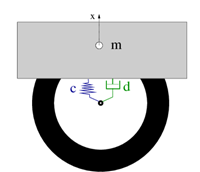
Als Beispiel soll hier das oft verwendete schwingungsfähige System eines Feder-Dämpfer-Masse Systems genutzt werden.
Schwingung
Das folgende Video erklärt die physikalische Zusammenhänge hinter einer harmonischen Schwingung sehr anschaulich.
Es spiegelt genau ein 1/4-Fahrzeug wider und ist daher für Fahrzeugtechniker besonders interessant. Analog kann das Beispiel eines RC-Netzwerks für die Elektrotechnik verwendet werden.
Die Schwingungsdifferentialgleichung leitet sich nach den Axiomen von Newton und d´Alembert nachfolgend her: Kraft = Masse * Beschleunigung.
Als Kräfte können hier die Federkraft FC und die Dämpfungskraft FD angesetzt werden. Diese sind proportional mit der Federkonstanten c und dem Federweg x bzw. der Dämpfungskonstante d und der Geschwindigkeit x’ mit welcher das Rad einfedert. Es ergibt sich:
Wird die Masse dividiert und für die Beschleunigung der Differentialquotient geschrieben, ergibt sich:
Die allgemeine Lösung dieser Differentialgleichung kann in der Literatur nachgeschlagen werden. Sie unterscheidet sich in Schwingfall, Kriechfall und aperiodischer Grenzfall. In keinem der Fälle kommt eine handliche, einfach zu bedienende Gleichung zur Anwendung. Selbst einfache Differentialgleichungen haben teils komplizierte allgemeine Lösungen. Auch das Übernehmen dieser Lösung(en) nach Excel stellt Schwierigkeiten dar, da die Formel nur schwer fehlerfrei in die Formelmaske übernommen werden kann.
Trick von Euler-Cauchy
Es empfiehlt sich den Ansatz nach Euler-Cauchy zu verwenden, in welchem der Differentialquotient dx/dt in vorheriger Gleichung durch den Differenzenquotient Δx/Δt ersetzt wird. Es ergibt sich:
Mit dieser Gleichung lässt sich die Geschwindigkeitsänderung pro Zeitänderung berechnen. Die Zeitdifferenz Δt sollte dabei relativ klein sein, damit eine numerische Lösung nicht zu große Abweichungen zur allgemeinen Lösung aufweist.
Berechnung in Excel
In der erste Zeile der Berechnung muss die Startbedingung festgelegt werden. Beispielhaft x=0m Auslenkung und eine Bewegung von x’=-2m/s.
In der zweiten Zeile kann dann die Geschwindigkeitsänderung Δx’ berechnet werden mit
Der Index i stellt jeweils die aktuelle Zeile dar, der Index i-1 folglich die vorherige Zeile. Dabei ist Δt die Zeitdifferenz von der vorherigen (i-1) Zeile, zur aktuellen (i).
Der Weg x kann durch numerische Integration berechnet werden.
Beispiel
Ein 1/4-Fahrzeug mit den Parametern
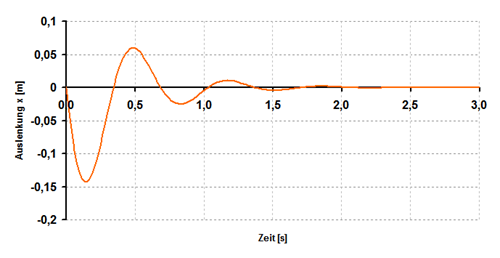
Es sei noch angemerkt, dass das Rad an sich ebenfalls ein schwingungsfähiges System ist. Der Reifen hat ebenfalls eine Feder- und Dämpfungskonstante, so dass die gesamte Schwingungsdifferentialgleichung zwischen Fahrbahn und Fahrzeug (jeweils 1/4-Fahrzeug) eine Schwingungsdifferentialgleichung 4. Ordnung ist. Weiterführende Berechnungen dazu unter: https://www.cbcity.de/schlagloch-von-der-strasse-zum-fahrer.