Motorblog
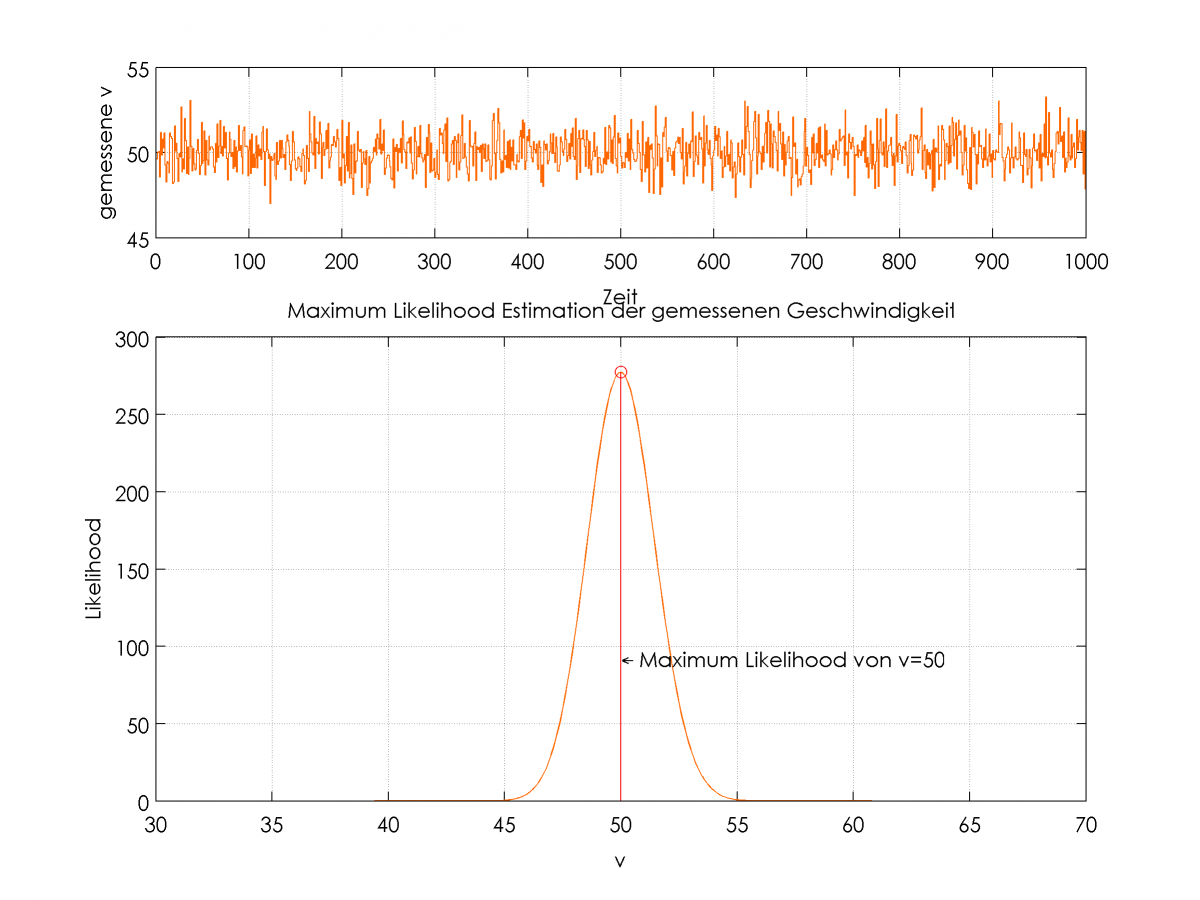
Erfasst man einen realen Vorgang mit einem Sensor, so hat man intuitiv das Gefühl, dass dieser Sensor den realen Wert ‘schon korrekt messen wird’. Das Problem ist, dass kein Sensor perfekt ist. Am Beispiel der Umfeldsensorik für PKW ist ein sehr populärer Sensor der Radar, welcher z.B. für die adaptive Geschwindigkeitsregelung ACC, Ein-/Ausparkassistenten oder auch Totwinkelassistenten eingesetzt wird.
Schaut man sich die Rohmesswerte eines solchen Sensors an, wird klar, was mit ‘nicht perfekt’ gemeint ist:
![Rohmessdaten eines Nahbereichsradarsensors für mehrere Radfahrer (blau) und KFZ (grün). Quelle: [Höringklee 2013 - Entwicklung eines Assistenzsystems zur Überwachung nicht einsehbarer Bereiche im Fahrzeugumfeld]](https://www.cbcity.de/wp-content/uploads/2013/08/Messdaten_Radarsensor_Draufsicht_Fahrrad_Kfz.png)
Rohmessdaten eines Nahbereichsradarsensors für mehrere Radfahrer (blau) und Fahrzeuge (grün), welche sich an den Sensor (schwarzes Kreuz links) annähern. Quelle: [Höringklee 2013 – Entwicklung eines Assistenzsystems zur Überwachung nicht einsehbarer Bereiche im Fahrzeugumfeld]
Ist dort etwas?
Kommt dort etwas?
Wie schnell ist es?
Was ist es?
Continue Reading
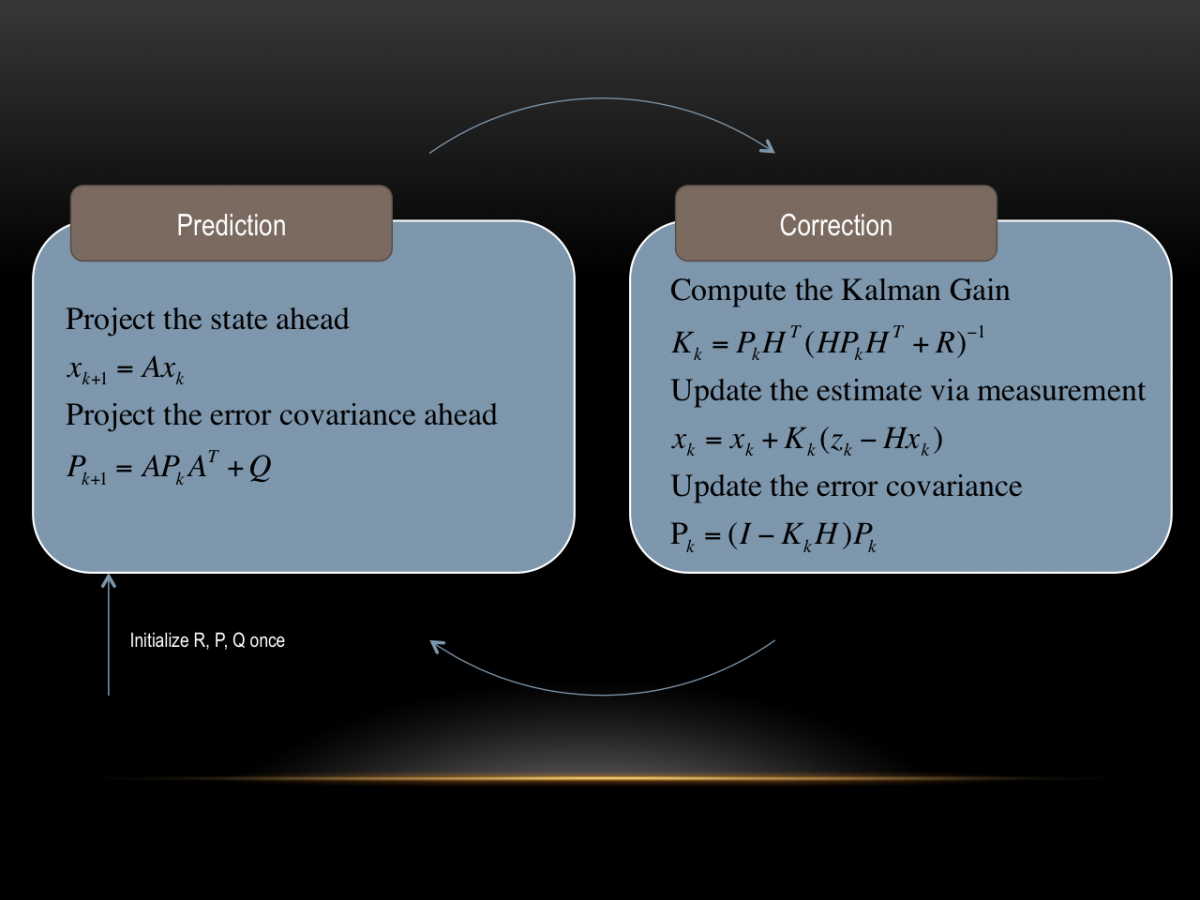
Nachdem wir im Teil 1 den Kern des Kalman Filters geklärt haben, widmen wir uns nun dem komplizierteren Teil. Die im Teil 1 genannte Vorgehensweise mit dem multiplizieren bzw. addieren der Mittelwerte und Varianzen funktioniert so nur im eindimensionalen Fall. \(\)
Das heißt, wenn der Zustand, den man messen möchte, mit nur einer Variablen vollständig beschrieben werden kann. Das Beispiel, welches eingangs genannt wurde, die Position eines Fahrzeugs im Tunnel zu bestimmen, kann aber nicht mehr mit einer Variablen vollständig beschrieben werden. Zwar interessiert nur die Position, aber diese ist genau genommen ja schon 2-Dimensional in der Ebene (\(x\) & \(y\)). Außerdem kann nur die Geschwindigkeit (\(\dot x\) & \(\dot y\)) gemessen werden, nicht die Position direkt. Dies führt zu einem 4D-Kalman-Filter, mit folgenden Zustandsvariablen:
$$x=\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}=\begin{matrix}\text{Position X} \\ \text{Position Y} \\ \text{Geschwindigkeit in X} \\ \text{Geschwindigkeit in Y}
\end{matrix}$$
Herr Kalman hatte sich nun überlegt, wie man es schafft, trotz verrauschter Messung einzelner Sensoren, eine optimale Schätzung aller Zustände zu berechnen.
Nehmen wir an man fährt mit seinem PKW Navi in einen Tunnel. Das GPS Signal ist weg. Trotzdem möchte man vielleicht angezeigt bekommen, dass man die Ausfahrt im Tunnel nehmen soll. Woher soll das Navi wissen, wo man gerade ist? Richtig: Es fusioniert die Fahrzeugsensoren und berechnet damit die Position so gut es geht.

Nun denkt man sich: OK, wenn ich zuletzt am Tunneleingang war und mit 50km/h fahre, dann kann das Navi ja exakt ausrechnen, wo (x=Position) man sich 1 Minute (t=Zeit) später befindet: