Motorblog
Einleitung
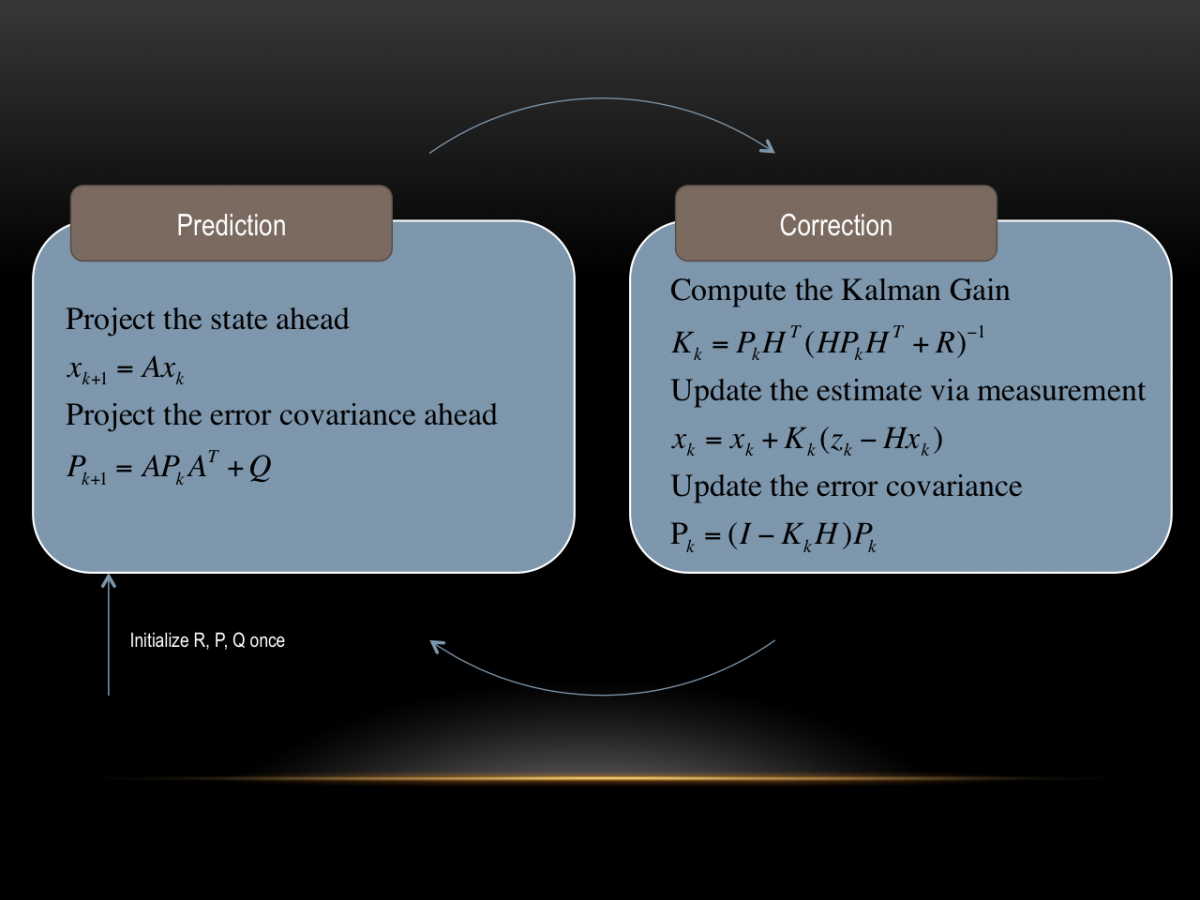
Für ein Vorstellungsgespräch bei meinem jetzigen Arbeitgeber habe ich unter anderem nach den gängigsten Filtern zur Beschreibung von Bewegungen im Raum gesucht. Dabei bin ich auf dieses 4D Kalman Filter gestoßen. Dort werden die mathematischen Zusammenhänge und die Implementierung des Filters in Matlab beleuchtet. Da ich bei meiner aktuellen Arbeitstelle allerdings mit C-Code arbeite, habe ich mir zum Ziel gesetzt, den Algorithmus in C umzusetzen.
Mein Vorschlag ist daher keine Kritik oder Neuentwicklung des besprochenen Filters an sich, sondern ist vielmehr als Ergänzung für Entwickler gedacht, die lieber in C arbeiten.
Der komplette Source-Code befindet sich hier. Abhängigkeiten zu externen (nicht-Standard-) Bibliotheken wurden gezielt vermieden, allerdings wurde an zwei Stellen externen Code mit in das Projekt eingebaut und entsprechend erwähnt. Dieser Filter kann durch einfache Änderungen als Basis für einen echten eingebetteten Filter hergenommen werden.
Ich werde hier Schritt für Schritt durch die wichtigsten Stellen des Codes gehen und an geeigneten Stellen auf den originalen Algorithmus verweisen.
Sollten programmiertechnische Fehler auffallen oder gar Copyright-Probleme entdeckt werden, bitte ich sehr darum, sich bei mir zu melden oder selbst über Github aktiv zu werden. Der Code wurde auf meiner Maschine mit meinem Compiler getestet, ein plattformübergreifendes Funktionieren kann nicht garantiert werden. Ich bin aber gerne für konstruktive Kritik offen!
Source Code
Inhalt von KalmanFilter.c
Zeilen 1 – 6
Benötigte Includes, hauptsächlich für Ein- und Ausgabe und zu selbstgeschriebener KalmanFilter.h-Datei.
Zeilen 15 – 26
Erzeugen von Zufallsvariablen. Benutzt wird die Box Muller Transformation zur Erzeugung Gauß-verteilter Zufallszahlen (entnommen von hier). Dies entfällt bei einem echten System.
Zeilen 29 – 37
Matrizen werden entsprechend dem Beispiel mit Anfangsdaten befüllt.
Zeilen 40 – 57
In diesen Matrizen werden Zwischenergebnisse gespeichert. Diese werden hier mit Nullen initialisiert.
Zeilen 59 – 62
Es wird eine Ergebnis-Datei geöffnet und der Gnuplot initialisiert.
Zeilen 64 – 112
Hauptschleife, die den Algorithmus implementiert. Kann im Falle einer echten Anwendung durch eine while-Schleife ersetzt werden, in der zyklisch Werte abgefragt und weiterverarbeitet werden. Das Abfragen der Werte kann in
Zeilen 78 + 79
geschehen.
Vor jedem Rechenschritt steht der Teil des originalen Algorithmus, der darunter berechnet wird. In
Zeilen 105 – 109
werden Zwischenschritte der Berechnung ausgegeben. Hier kann man zu Debug-Zwecken auch andere Werte verwenden.
Zeilen 115 – 121
Housekeeping
Zeilen 125 bis Ende
Der Rest des C-Files implementiert die nötigen Algorithmen. Bei den meisten handelt es sich um einfache Matrix-Multiplikationen oder Ausgabefunktionen. Die einzig kompliziertere Rechnung ist die der Matrix-Inversen (entnommen von hier). Durch die Ausgabe im gnuplot und als Textdatei, kann der Entwickler schnell und einfach feststellen, dass er richtig entwickelt hat. Im Falle dieses Algorithmus habe ich so recht einfach meinen Output mit dem des Originaloutputs vergleichen können.
Inhalt von KalmanFilter.h
Enthält
Ab Zeile 10
hauptsächlich Funktionsdeklarationen der im vorhergehenden Teil beschriebenen Funktionen.
Ab Zeile 86
werden nützliche Abkürzungen definiert, die den Hauptcode etwas aufgeräumter wirken lassen sollen. Der Schlüssel #define weist den Compiler an, den nachfolgenden String VOR dem Compilieren durch den darauffolgenden String zu ersetzen.
Beispiel:
#define WRITEFLOATARRAYTOFILE(f, arr) int i; for ( i= 0; i < SIZEOFARRAY(arr); i++) fprintf(f, "%f\n", arr[i]);
Schreibt die Werte eines Float-Arrays (arr) in eine Textdatei (f), mit jeweils einem Zeilenvorschub (\n) unter Zuhilfenahme eines weiteren hilfreichen Shortcuts SIZEOFARRAY (da die Größe eines Arrays in C nicht ohne Umwege zu erhalten ist). Im Code ist diese Funktionalität durch die Abkürzung WRITEFLOATARRAYTOFILE(f, arr) zu erreichen.
Inhalt von CleanMakeAndRun.bat
Dieses Skript entfernt zuvor gebaute Objekte und Executables und baut den Source Code neu. Außerdem wird er nach dem Bauen ausgeführt und das eventuell schon vorhandene gnuplot Fenster vor dem Ausführen geschlossen. So kann nach Änderungen am Code im gleichen Fenster neu gecleanet, gebaut und ausgeführt werden; alles mit einem Tastendruck.
Wie das funktioniert, wird im folgenden Video dargestellt.
Inhalt von Makefile
Eigentliche Anweisungen an den Compiler. Muss bei Hinzufügen, Ändern oder Löschen von Source-Code angepasst werden.
Inhalt von Kalman.m
Leicht angepasster Original-Algorithmus von hier.
Abhängigkeiten
Das Programm muss mit einem geeigneten C-Compiler compiliert werden. Ich selbst benutze MinGW auf Windows 10. Falls gnuplot zur Anzeige der Daten genutzt werden soll, ist die Installation von gnuplot erforderlich.
Vergleich der Output-Daten
Wie besprochen, handelt es sich im hier vorgeschlagenen Beitrag um eine Code-Portierung von Matlab auf C. Die folgenden Bilder zeigen, dass beide Algorithmen sich mit gleich parametriertem Filter in etwa gleich verhalten. Da es sich in beiden Fällen um “echte” Zufallszahlen handelt, kann nie der exakt gleiche Output erwartet werden.
Folgende Abbildung zeigt den Output des originalen Matlab-Algorithmus.
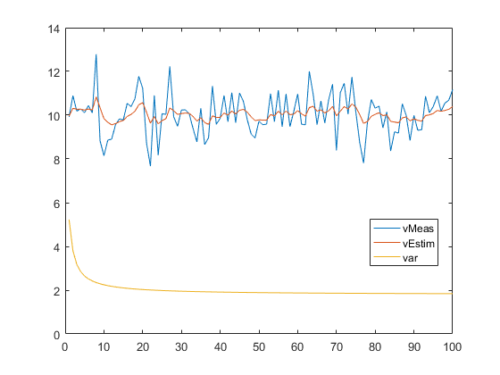
Der vorgeschlagene Ansatz in C liefert folgenden Output:
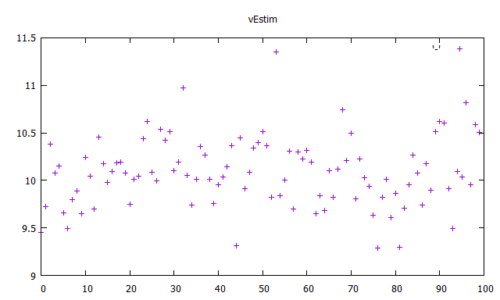
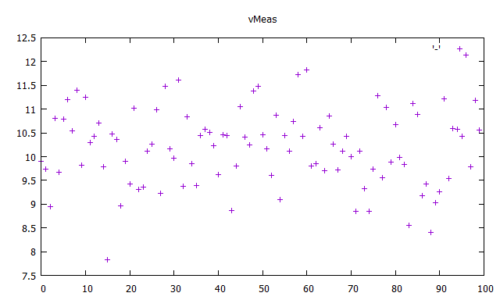
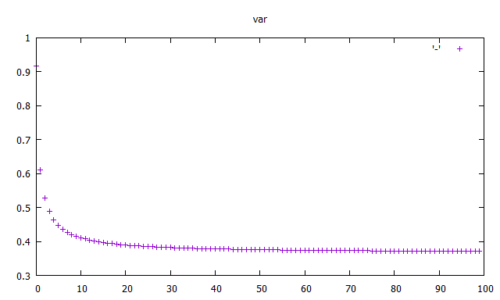
Wie schon viele von euch habe ich mich im Rahmen meines eigenen Projektes mit dem Kalmanfilter beschäftigt und dabei viel von den Blogeinträgen KF 1/KF 2/EKF gelernt. Da ich auch aufgrund des Standortvorteils direkt mit Paul über die Gestaltung fachsimpeln konnte, ist zwischen uns die Idee enstanden euch meine Umsetzung nicht vorzuenhalten. Deswegen möchte ich im Folgenden genauer auf die Bedatung der verschiedenen Matrizen, aber weniger auf die Berechnungen eingehen. Dafür sind ja schon die genannten Einträgen da.
Mit Abstand am häufigsten gelesen hier im Blog, sind die Beiträge zum Kalman Filter (Teil 1 & Teil 2 & EKF). In den Kommentaren und Emails, die ich dazu bekomme, zeigt sich allerdings, dass da mit Kanonen auf Spatzen geschossen wird. Einige Probleme, die der Algorithmus lösen soll, sind gar nicht so kompliziert, dass man einen Kalman Filter oder Extended Kalman Filter aufsetzen muss.
Ich möchte in diesem Beitrag den kleinen Bruder vom Kalman Filter, den Alpha-Beta-Filter, vorstellen. Dieser ist zwar im Grunde ein Kalman-Filter, allerdings mit einigen Vereinfachungen, sodass er leichter zu implementieren ist.
OK, jeder Ingenieur hat nach der Ankündigung “Timo Boll gegen KUKA Roboter” und dem imposanten Teaser Video wahrscheinlich ein lächeln im Gesicht gehabt. KUKA, das deutsche mittelständische Unternehmen einen YouTube Hit? Richtig gutes Marketing? Wow, das kann was werden.
Doch dann die Ernüchterung: Das angekündigte Match war doch nur ein “Werbespot“. Doch wieso eigentlich?
Das Problem am Tischtennis spielen gegen einen Roboter ist eigentlich nicht die Roboterbewegung sondern etwas ganz anderes.
Da die Beiträge zum Kalman Filter (Teil1 und Teil2) sowie der Beitrag zum Extended Kalman Filter die am Häufigsten gelesenen des Motorblogs sind, habe ich zum Extended Kalman Filter noch mal einen etwas detaillierteren Screencast aufgezeichnet, welcher recht ausführlich erläutert, wie dieser aufgesetzt wird und arbeitet.
Extended Kalman Filter with CTRV Vehicle Model in Python from Paul Balzer on Vimeo.
Nachdem wir im Teil 1 den Kern des Kalman Filters geklärt haben, widmen wir uns nun dem komplizierteren Teil. Die im Teil 1 genannte Vorgehensweise mit dem multiplizieren bzw. addieren der Mittelwerte und Varianzen funktioniert so nur im eindimensionalen Fall. \(\)
Das heißt, wenn der Zustand, den man messen möchte, mit nur einer Variablen vollständig beschrieben werden kann. Das Beispiel, welches eingangs genannt wurde, die Position eines Fahrzeugs im Tunnel zu bestimmen, kann aber nicht mehr mit einer Variablen vollständig beschrieben werden. Zwar interessiert nur die Position, aber diese ist genau genommen ja schon 2-Dimensional in der Ebene (\(x\) & \(y\)). Außerdem kann nur die Geschwindigkeit (\(\dot x\) & \(\dot y\)) gemessen werden, nicht die Position direkt. Dies führt zu einem 4D-Kalman-Filter, mit folgenden Zustandsvariablen:
$$x=\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}=\begin{matrix}\text{Position X} \\ \text{Position Y} \\ \text{Geschwindigkeit in X} \\ \text{Geschwindigkeit in Y}
\end{matrix}$$
Herr Kalman hatte sich nun überlegt, wie man es schafft, trotz verrauschter Messung einzelner Sensoren, eine optimale Schätzung aller Zustände zu berechnen.
Nehmen wir an man fährt mit seinem PKW Navi in einen Tunnel. Das GPS Signal ist weg. Trotzdem möchte man vielleicht angezeigt bekommen, dass man die Ausfahrt im Tunnel nehmen soll. Woher soll das Navi wissen, wo man gerade ist? Richtig: Es fusioniert die Fahrzeugsensoren und berechnet damit die Position so gut es geht.

Nun denkt man sich: OK, wenn ich zuletzt am Tunneleingang war und mit 50km/h fahre, dann kann das Navi ja exakt ausrechnen, wo (x=Position) man sich 1 Minute (t=Zeit) später befindet: