Motorblog
[Tutorial] Ermittlung der Rotationsmatrix zur Transformation zwischen sensorfestem und fahrzeugfestem Koordinatensystem
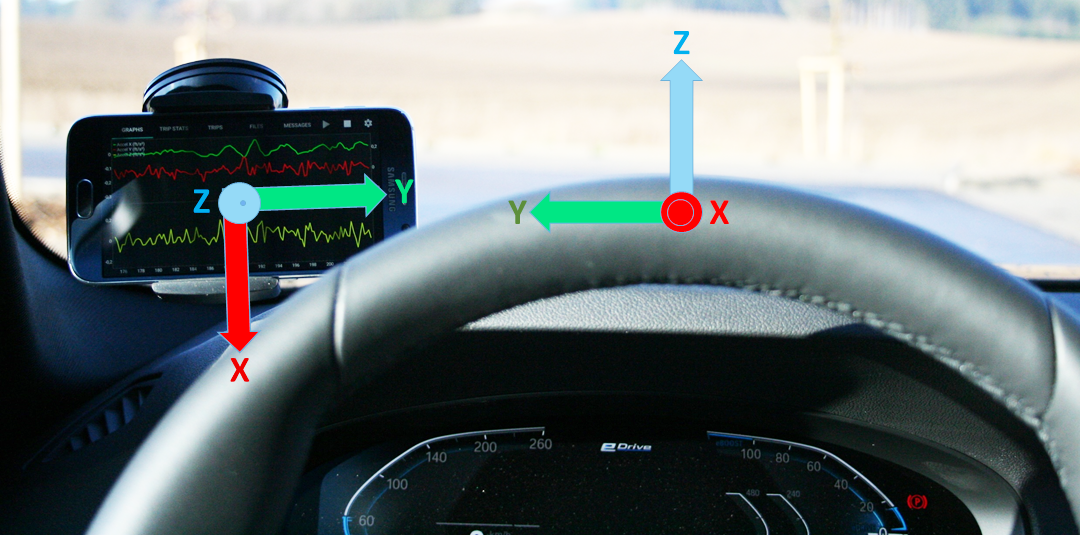
Viele interessante Artikel befassen sich mit der Rotationsmatrix und wie man diese zur Transformation zwischen Koordinatensystemen verwenden kann. Für meinen konkreten Anwendungsfall – der Auswertung von fahrdynamischen Messdaten im Fahrzeugbetrieb – konnte ich jedoch kein “Kochrezept” finden welches mir bei der Umrechnung von gemessenen Beschleunigungswerten aus dem gedrehten, sensorfesten Koordinatensystem in das fahrzeugfeste Koordinantensystem weiterhelfen konnte.
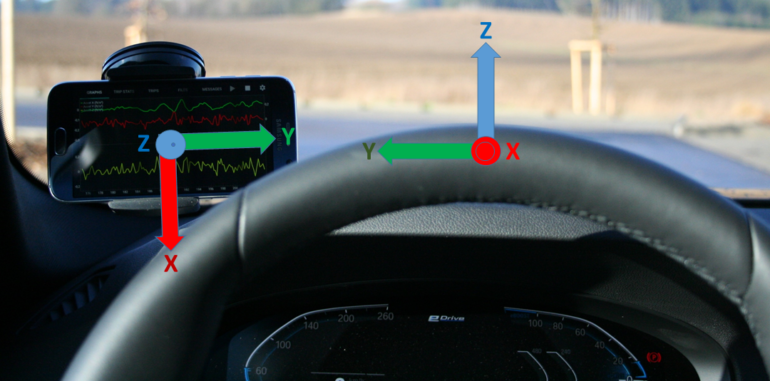
Darstellung der Smartphone-Position und der daraus resultierenden Verschiebung der Beschleunigungsachsen zwischen sensorfestem und fahrzeugfestem Koordinatensystem
Auf meinem Weg der Informationsbeschaffung bin ich unter anderen auch immer wieder auf den Motorblog-Beitrag von Paul Balzer und die Verlesungsvideos von Prof. Dr.-Ing. Jörg J. Buchholz zurückgekommen und habe im direkten Austausch wertvolle Tipps erhalten. Dabei ist auch das Angebot dieses Gastbeitrags entstanden, welches ich hiermit gerne wahrnehme um zu erläutern mit welcher Verfahrensweise ich einen Lösungsweg gefunden habe.
Wie schon viele von euch habe ich mich im Rahmen meines eigenen Projektes mit dem Kalmanfilter beschäftigt und dabei viel von den Blogeinträgen KF 1/KF 2/EKF gelernt. Da ich auch aufgrund des Standortvorteils direkt mit Paul über die Gestaltung fachsimpeln konnte, ist zwischen uns die Idee enstanden euch meine Umsetzung nicht vorzuenhalten. Deswegen möchte ich im Folgenden genauer auf die Bedatung der verschiedenen Matrizen, aber weniger auf die Berechnungen eingehen. Dafür sind ja schon die genannten Einträgen da.
Als Ingenieur ist man von der Informatik meilenweit entfernt. Im Studium wird man manchmal an Mathworks Matlab herangeführt, versteht es aber im Allgemeinen erstmal nicht. In Fleisch und Blut geht es ohnehin nie über, weil es nahezu unbeschränkte Möglichkeiten bietet, das Studium aber nur eine kurze Zeit dauert.
Während man die ersten Semester Diagramme und Protokolle lieber mit Excel erstellt, reduziert sich die Zeit, in welcher man sich mit Matlab beschäftigen kann, noch weiter. In den letzten Semestern, vielleicht erst in der Diplomarbeit, merkt man dann aber, dass es echt gut ist! Warum nicht eher?
Kommt man aus dem Uni-Umfeld heraus, wird es leider sehr teuer mit Matlab! Eine Standard Einzelplatz Lizenz ohne eine einzige Toolbox kostet 2.000€ Netto. Nur um ein paar Diagramme zu erstellen?
Ich habe mir daher vor einiger Zeit Python angesehen, welches nach einiger Zeit zunehmend Spaß macht! Da es zu Beginn relativ schwer war, einen Einstieg zu finden, möchte ich mein Setup mal vorstellen.
Python
Das Herz der Angelegenheit und bei Linux, Unix und MacOS schon von Haus aus an Board. Für Windows muss man es manuell nachinstallieren. Generell ist die einfachste Variante Anaconda zu installieren, weil dort so ziemlich alle Pakete (Plug-Ins) dabei sind, die wichtig werden für die tägliche Arbeit.
In der Kommandozeile oder im Terminal kann man nun Python nutzen.
Plug-Ins
Python an sich ist nun schon mächtig, aber immernoch ein zahnloser Tiger, so lange es ohne Zusatzpakete auskommen muss. Zum installieren der Pakete kann man auf Paketmanager zurückgreifen, die die Arbeit in den meisten Fällen übernehmen. Hat man Anaconda installiert, sind die meisten Pakete schon dabei.
PIP Paketmanager
Der Paketmanager, welcher nachfolgend die Arbeit der Installation/Upgrades übernimmt, ist PIP. Die Installation von PIP erfolgt betriebssystemabhängig. Am einfachsten mit der get-pip.py, welche dort herunter geladen werden kann. Da wir ja Python installiert haben, können wir einfach:
python get-pip.py
eingeben, dann müsste alles automatisch funktionieren. Da es nun für jedes Betriebssystem immer ein paar Unterschiede gibt, möchte ich aus diesem Beitrag kein Installationstutorial machen, sondern einfach nur zeigen, was meiner Meinung nach am besten geeignet ist, ohne Support.
Scipy
Das wichtigste Paket, wenn man in großen Schritten Richtung Matlab gehen möchte: Scipy. Es enthält viele elementare Pakete, wie z.b.
- Matplotlib zum Erstellen von Plots
- IPython zum angenehmen arbeiten
- Numpy zur effizienten und einfachen numerischen Berechnung
Arbeitsumgebung IPython
Ich habe einige Python IDEs ausprobiert, aber bin nun bei IPython hängen geblieben. IPython kommt mit Scipy mit und ist sehr umfangreich. Gestartet wird die Arbeitsumgebung über die Kommandozeile mit
ipython notebook --script
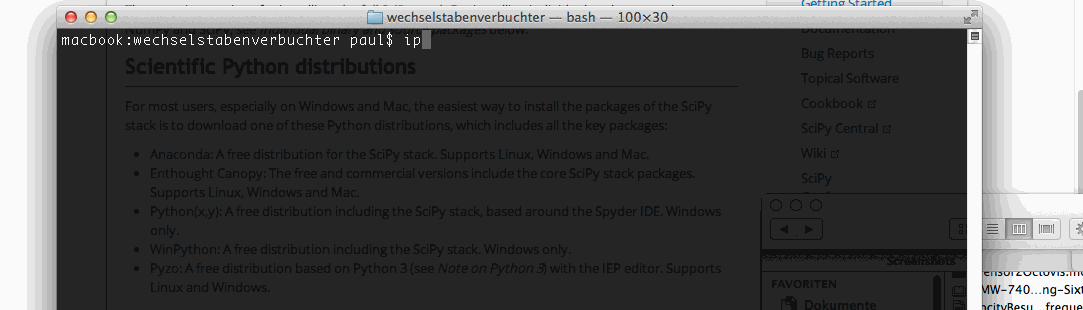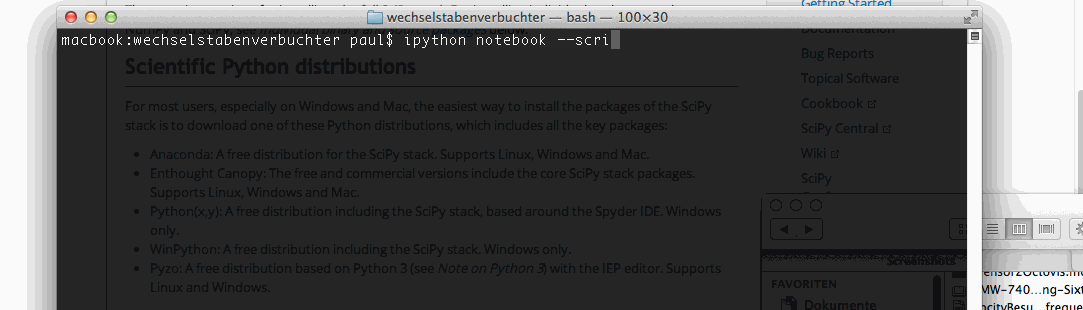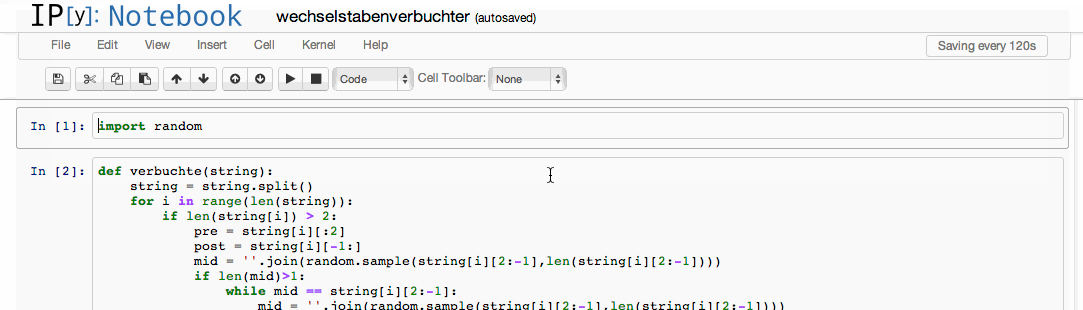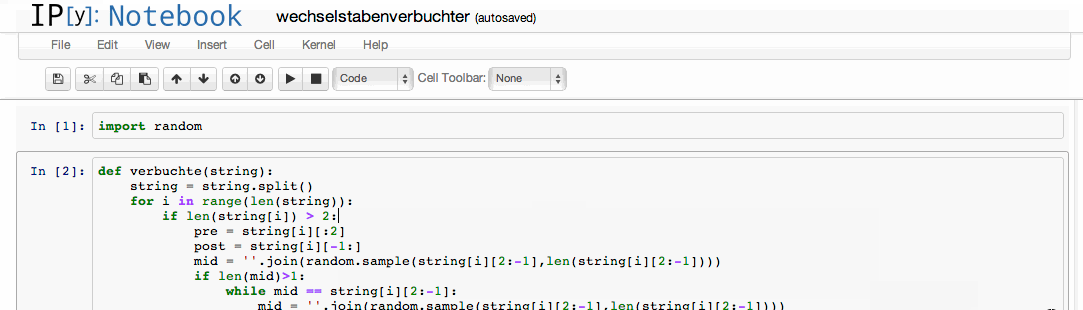
Der Befehl notebook startet einen lokalen Server, welcher über den Browser unter localhost angesprochen werden kann. Auf der ‘Webseite’ ist es dann möglich so genannte Notebooks zu öffnen, welche ähnlich wie MATLAB .m Files zu nutzen sind. Der Schalter –script sorgt dafür, dass immer parallel eine .py (also eine Python Datei) gespeichert wird, wenn man das Notebook (.ipynb) speichert.
Import
Der große Unterschied zu MATLAB ist nun, dass man bei Python immer erst mal sagen muss, welche Plug-Ins man nutzen möchte im aktuellen Projekt (ähnlich der ‘path’ Umgebung in MATLAB). Möchte man beispielsweise ein Plot erstellen, so ist vorher mitzuteilen, dass die mit Scipy gelieferte Bibliothek Pyplot zu verwenden ist.
import matplotlib.pyplot as plt
Danach stehen alle Funktionen von Matplotlib unter dem Objektnamen plt zur Verfügung.
Plot erstellen
Ein Plot lässt sich beispielsweise erstellen mit
x=range(5) y=range(5) plt.plot(x,y) plt.show()
Diese Bibliothek ist sehr mächtig, wie die Beispiele zeigen!
Beispiel
import numpy as np
import matplotlib.pyplot as plt
import random
import time
n = 1100000
m=0.0
v=0.0
elapsed=[]
vals=[]
for i in xrange(0,n,1000):
# Python reagiert auf Einrückungen (Leerzeichen oder <tab>)
# Alles was eingerückt ist, gehört zur Schleife!
#print 'Berechne für ' + str(i) + ' Werte.'
values = np.random.sample(i)
start = time.clock()
m = np.mean(values)
v = np.var(values)
elapsed.append((time.clock() - start))
vals.append(i)
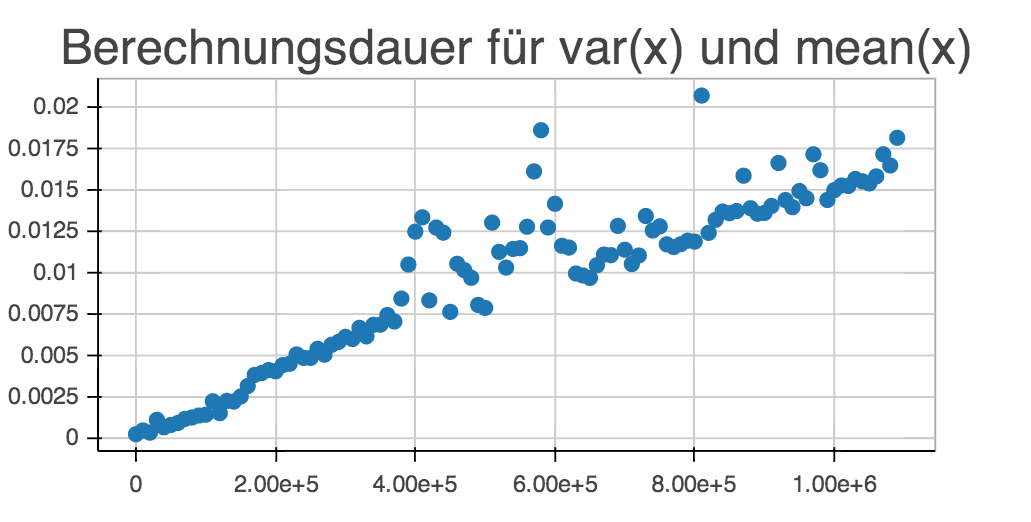
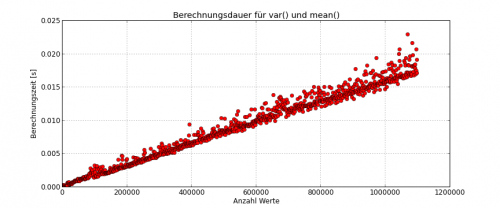
fig = plt.figure(figsize=(12,5))
plt.plot(vals,elapsed, 'ro')
plt.xlabel(u'Anzahl Werte')
plt.grid()
plt.ylabel(u'Berechnungszeit [s]')
plt.title(u'Berechnungsdauer für var() und mean()')
plt.savefig('Berechnungsdauer.png',dpi=72)
plt.close()
print('Done.')
Zusatzbibliotheken machen Python mächtig
Zwar gibt es für MATLAB unzählige Toolboxen und auch das Matlab Central, wo Zusatzfunktionen herunter geladen werden können, aber der große Vorteil an Python ist: Es ist kostenfrei!
Ein Blick auf die kompilierten Windows Versionen der Pakete zeigt, dass man überhaupt nicht überblicken kann, was alles möglich ist. Die Pakete die ich bisher genutzt habe, sind folgende:
- Pandas, der Allrounder und mit Abstand das wichtigste Paket, wenn es um Datenhandling (Zeitreihen usw.) geht
- Numpy um Vektoren und Arrays effizient zu benutzen
- requests um Anfragen an Server stellen zu können
- BeautifulSoup um HTML Antworten einfach auslesen zu können
- Basemap um Karten zu erstellen
- simplekml um Google Earth .kml Dateien zu erstellen
- Bokeh für schönere Plots, Interaktivität und HTML Export
Schönere Plots
Möchte man das Plot jetzt auch noch mal in “schön” haben, so bietet sich Bokeh an. Es muss natürlich importiert werden
from bokeh.plotting import *
aber anschließend geht es sogar einfacher und ansehnlicher als mit Matplotlib:
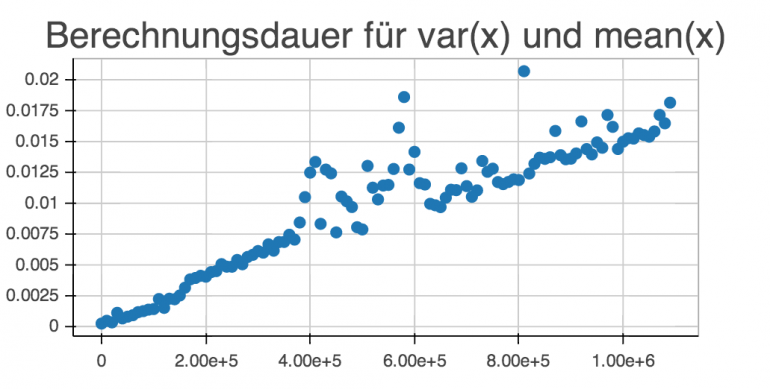
scatter(vals, elapsed, title='Berechnungsdauer') show()
Learning by Doing
Weiterführend ist der Kurs “Introduction to scientific computing with Python” von J.R. Johansson empfohlen! Hier insbesondere der Teil 4: matplotlib – 2D and 3D plotting in Python.
Nachteil ggü. MATLAB
Der Nachteil ist ganz eindeutig, dass viele viele viele verschiedene Menschen die Zusatzpakete erstellen und jeder so seine eigene Art hat, dies umzusetzen. Das führt dazu, dass zum einen die Webseiten, wo die Pakete zu bekommen sind, nicht einheitlich aussehen und teilweise wirklich schlecht gepflegt werden (Installationshinweise usw..) und zum anderen auch die Art, wie man die Pakete nutzen kann, verschieden ist.

Bei MATLAB ist alles zentral durch Mathworks organisiert, d.h. man kann sich drauf verlassen, dass es eine ordentliche Hilfe gibt, dass die Funktion genau so funktioniert wie dort dargestellt und das es vom Syntax her eindeutig ist.
Bei einigen Python Paketen ist es eher ein Rätselraten, wie man das nun so benutzt, dass es macht was man möchte. Da wird http://stackoverflow.com/ schnell der beste Freund!
Erfasst man einen realen Vorgang mit einem Sensor, so hat man intuitiv das Gefühl, dass dieser Sensor den realen Wert ‘schon korrekt messen wird’. Das Problem ist, dass kein Sensor perfekt ist. Am Beispiel der Umfeldsensorik für PKW ist ein sehr populärer Sensor der Radar, welcher z.B. für die adaptive Geschwindigkeitsregelung ACC, Ein-/Ausparkassistenten oder auch Totwinkelassistenten eingesetzt wird.
Schaut man sich die Rohmesswerte eines solchen Sensors an, wird klar, was mit ‘nicht perfekt’ gemeint ist:
![Rohmessdaten eines Nahbereichsradarsensors für mehrere Radfahrer (blau) und KFZ (grün). Quelle: [Höringklee 2013 - Entwicklung eines Assistenzsystems zur Überwachung nicht einsehbarer Bereiche im Fahrzeugumfeld]](https://www.cbcity.de/wp-content/uploads/2013/08/Messdaten_Radarsensor_Draufsicht_Fahrrad_Kfz.png)
Rohmessdaten eines Nahbereichsradarsensors für mehrere Radfahrer (blau) und Fahrzeuge (grün), welche sich an den Sensor (schwarzes Kreuz links) annähern. Quelle: [Höringklee 2013 – Entwicklung eines Assistenzsystems zur Überwachung nicht einsehbarer Bereiche im Fahrzeugumfeld]
Ist dort etwas?
Kommt dort etwas?
Wie schnell ist es?
Was ist es?
Continue Reading
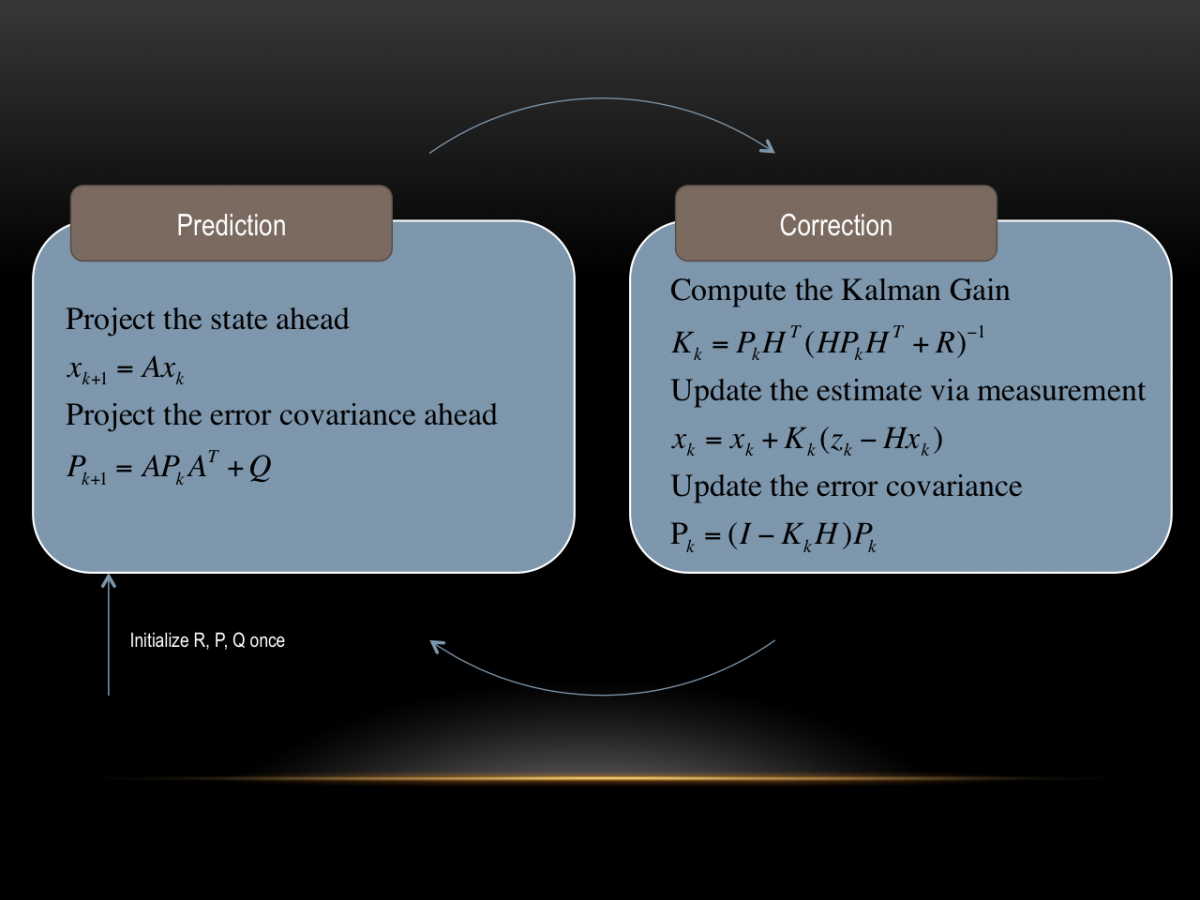
Nachdem wir im Teil 1 den Kern des Kalman Filters geklärt haben, widmen wir uns nun dem komplizierteren Teil. Die im Teil 1 genannte Vorgehensweise mit dem multiplizieren bzw. addieren der Mittelwerte und Varianzen funktioniert so nur im eindimensionalen Fall. \(\)
Das heißt, wenn der Zustand, den man messen möchte, mit nur einer Variablen vollständig beschrieben werden kann. Das Beispiel, welches eingangs genannt wurde, die Position eines Fahrzeugs im Tunnel zu bestimmen, kann aber nicht mehr mit einer Variablen vollständig beschrieben werden. Zwar interessiert nur die Position, aber diese ist genau genommen ja schon 2-Dimensional in der Ebene (\(x\) & \(y\)). Außerdem kann nur die Geschwindigkeit (\(\dot x\) & \(\dot y\)) gemessen werden, nicht die Position direkt. Dies führt zu einem 4D-Kalman-Filter, mit folgenden Zustandsvariablen:
$$x=\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}=\begin{matrix}\text{Position X} \\ \text{Position Y} \\ \text{Geschwindigkeit in X} \\ \text{Geschwindigkeit in Y}
\end{matrix}$$
Herr Kalman hatte sich nun überlegt, wie man es schafft, trotz verrauschter Messung einzelner Sensoren, eine optimale Schätzung aller Zustände zu berechnen.
Nehmen wir an man fährt mit seinem PKW Navi in einen Tunnel. Das GPS Signal ist weg. Trotzdem möchte man vielleicht angezeigt bekommen, dass man die Ausfahrt im Tunnel nehmen soll. Woher soll das Navi wissen, wo man gerade ist? Richtig: Es fusioniert die Fahrzeugsensoren und berechnet damit die Position so gut es geht.

Nun denkt man sich: OK, wenn ich zuletzt am Tunneleingang war und mit 50km/h fahre, dann kann das Navi ja exakt ausrechnen, wo (x=Position) man sich 1 Minute (t=Zeit) später befindet:
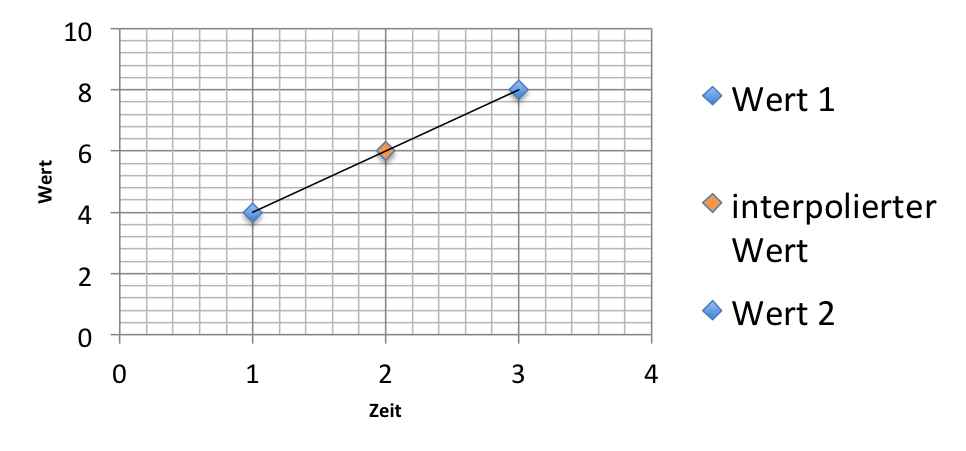
Interpolation hat fast jeder schon einmal gehört. Man benötigt zu bestehenden Messwerten eine feiner Auflösung und bestimmt Zwischenstellen linear, polynomisch oder mittels Spline. Im nachfolgenden Bild ist eine lineare Interpolation (orange) zu bestehenden Messwerten (blau) zu sehen.
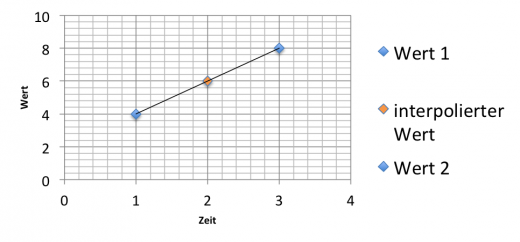
Orangener Wert ist linear interpoliert zu den bestehenden blauen Werten
Es gibt allerdings auch noch wesentlich ausgeklügeltere Verfahren der Interpolation, mit dessen Hilfe man erstaunliche Ergebnisse erzielen kann. Im Folgenden soll beispielhaft die Interpolation einer harmonischen Schwingung mit Matlab erfolgen.
Ein Thema, was mich schon lange beschäftigt, was aber wahrscheinlich die wenigsten Menschen überhaupt interessieren dürfte, möchte ich in diesem Beitrag mal abhandeln. Es geht dabei um das Differenzieren verrauschter Signale. Da stellt sich natürlich die Frage: Wo kommt so etwas überhaupt vor? An unglaublich vielen Stellen kommt das vor. Immer wenn man von einer gemessenen Größe auf eine andere schließen möchte, welche differenziellen Zusammenhang hat. Beispielsweise bei der Leistungsmessung auf einem Rollenleistungsprüfstand oder wenn man aus Positionsangaben einer GPS Messung die Geschwindigkeit berechnen möchte oder oder oder.

Der ein oder andere hat sich vielleicht schon mal gefragt, was am Autoradio die Knöpfe AM und FM bedeuten, kommen doch bei beiden mehr oder weniger gute Radiosender an. Es handelt sich dabei um verschiedene Verfahren, mit welchen die Radiostationen ihre Audiosignale Codieren, um sie über Funk durch die Luft an das Autoradio zu senden.

Diese Codierung ist notwendig, weil Sprache, Musik und unsere Ohren in einem Frequenzbereich von 20…20.000Hz arbeiten. Geht man einige Meter von einem sprechenden Menschen weg, so ist er kaum noch zu verstehen. Die Dämpfung von Audiosignalen in der Luft ist erheblich, in diesem Frequenzbereich kann Radio also nicht übertragen werden. Das Audiosignal muss an der Quelle codiert werden, damit es über weitere Strecken übertragen werden kann. Eines dieser Verfahren, wenn auch ein sehr sehr einfaches, ist die so genannte Amplitudenmodulation AM.
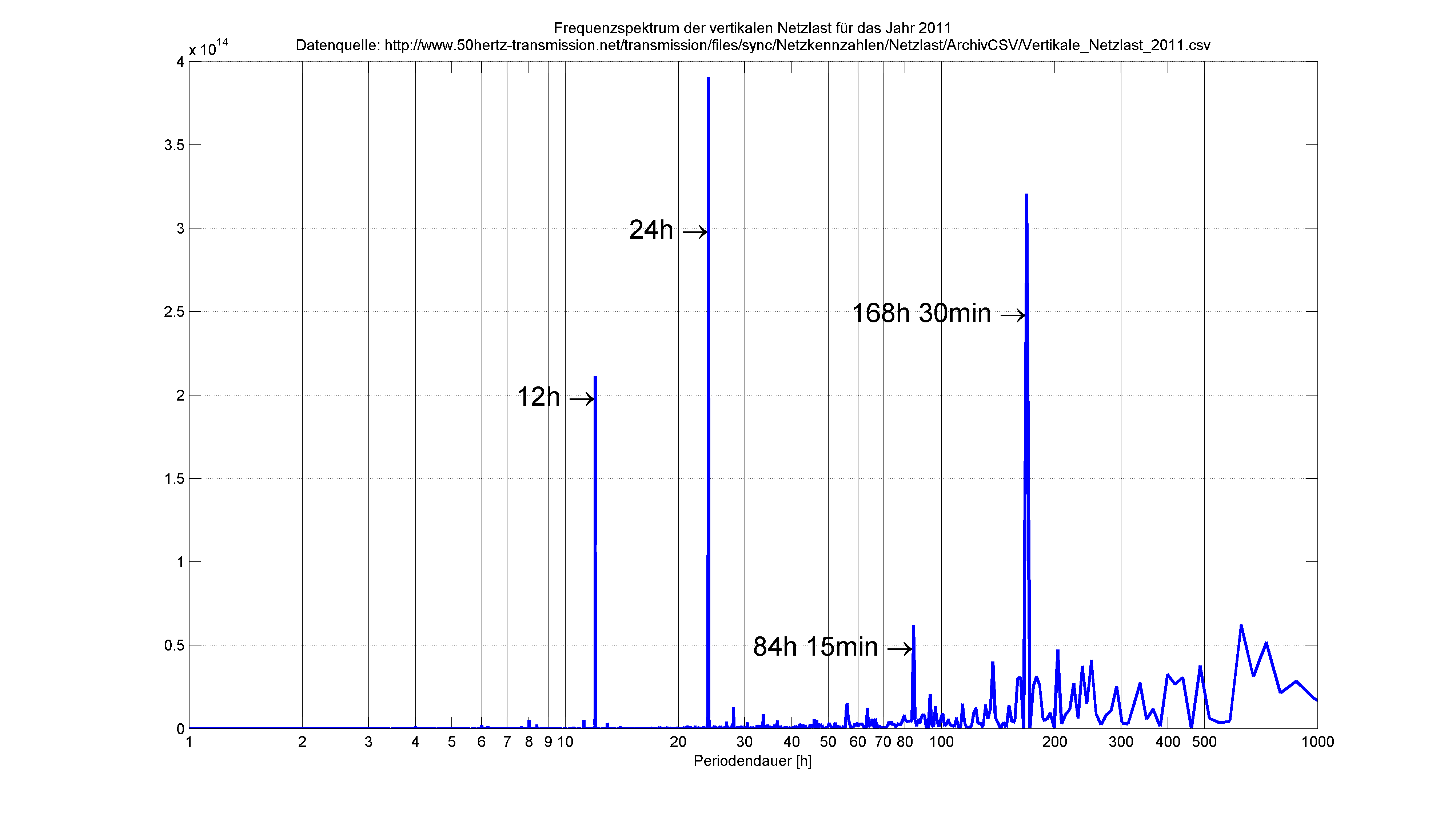
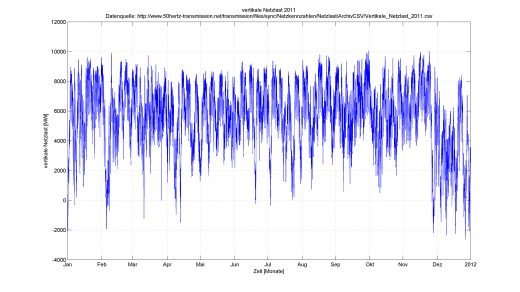
Um technische Sachverhalte beurteilen zu können, bietet es sich an, diese erst einmal zu messen. Die physikalische Größe wird also vom Computer diskret (d.h. nur “alle paar Millisekunden” oder “1x im Jahr” oder “jede 15min”) abgespeichert und kann dann weiter verarbeitet werden. Beispielhaft hier die vertikale Netzlast des deutschen Stromnetzes von 2011:
Möchte man dieses gemessene Signal jetzt auf beinhaltende Frequenzanteile untersuchen, so wurde vom genialen und zu seiner Zeit verkannten Mathematiker Joseph Fourier, die nach ihm benannte Fourier-Analyse entwickelt, welche das exzellent erledigt.
Man kann es ja nicht leugnen, so ein Starr-Rahmen sieht einfach klasse aus. Das findet der Prüfer beim DEKRA oder TÜV auch, aber er sieht die Gefahren. Welche das sind, wird bei folgender einfachen Berechnung deutlich.
Die Variante, die Daten über ein Videobild zu legen, ist ähnlich, wie mit Kanonen auf Spatzen zu schießen. Das sieht zwar schön aus, aber ist sehr viel Aufwand. Oft reicht es auch aus, die Daten in Diagrammen darzustellen.
Im Folgenden möchte ich zeigen, wie man Daten aus einer Datei in anschauliche Diagramme verpackt und automatisiert abspeichert.
Ich hatte vor ein paar Tagen die Möglichkeit auf einem heißen Sitz platz zu nehmen. Genauer gesagt auf dem Beifahrersitz eines BMW M3 3.2 E36, welcher von einem geschätzten Kollegen über den Eurospeedway Lausitzring bewegt wurde. Dazu habe ich mir eine Kamera und eine V-Box Mini geschnappt (danke an alle Beteiligten!) und ein paar Fahrdynamikdaten aufgezeichnet.

Wenn man genug Kleingeld hat, kann man ein fix und fertiges System kaufen, mit welchem Daten+Video synchron aufgezeichnet werden. Racelogic hat das z.B. im Angebot. Ich möchte im Folgenden zeigen, wie man aus Video und Daten trotzdem eine annehmbare Datenvisualisierung produzieren kann.

Regelungstechnik ist nicht unbedingt ein Haupteinsatzgebiet der Fahrzeugtechniker. Immerhin ist es ja auch eine eigenständige Studienrichtung im Fachgebiet der Automatisierungstechnik. Da sind die Profis zu finden.
Dennoch sei mir an dieser Stelle gegönnt einen Einblick in diese interessante Fachrichtung zu geben.