Nachdem im Teil1 und Teil2 das Kalman Filter eindimensional sowie mehrdimensional erläutert wurde, geht es jetzt in diesem Teil3 der Kalman Filter Reihe um den Klassiker: Das Extended Kalman Filter.
Dieses Filter ist das wohl am häufigsten anzutreffende Filter, wenn es um die Messung oder Beobachtung von realen Prozessen mit realen Sensoren geht. Weshalb? Weil fast jeder Sensor verrauschte Messwerte ausgibt und fast jeder Prozess mit mathematischen Gleichungen beschrieben werden kann.
Diese Gleichungen sind aber oftmals nichtlinear, weshalb das normale Kalman Filter nicht mehr verwendet werden kann.
Beispiel: Fahrzeug im Tunnel ohne GPS Empfang

Ein Fahrzeug fährt mit (fest verbautem) Navigationsgerät in einen Tunnel und verliert das Signal zur Positionsbestimmung. Trotzdem weiß das Navi, wo die Ausfahrt ist. Wie das?
Der Trick (und Preisunterschied) zum portablen Navi ist, dass das fest verbaute Navigationsgerät ja noch Verbindung zum Fahrzeug hat und z.B. die Fahrgeschwindigkeit über die Raddrehzahlsensoren sowie die Drehung des Fahrzeugs über den Gierratensensor (aus dem ESP System) als Messgrößen zur Verfügung hat. Damit lässt sich mit ein wenig Mathematik und eben Sensordatenfusion eine Ortsinformation berechnen, obwohl diese gar nicht mehr gemessen werden kann.
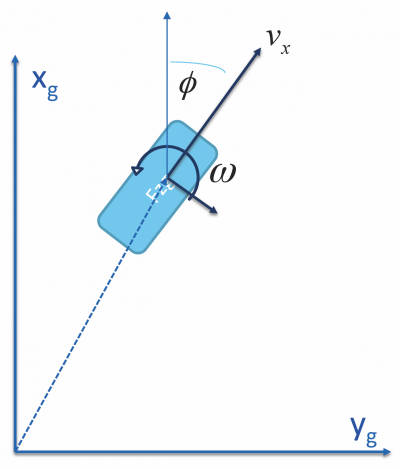
Fahrzeuggeschwindigkeit vx, Drehrate ω, Fahrtrichtungswinkel φ, globale Koordinaten xg und yg (auch Länge und Breite genannt).
Lokal
Die Fahrgeschwindigkeit wird in Fahrzeuglängsrichtung gemessen, die Drehrate (Gierrate) um die Hochachse in der Nähe des Fahrzeugschwerpunkts über die ESP Sensorik.
\(\begin{matrix}\dot x = v_x \\ \dot y = 0 \\ \dot \phi = \omega \end{matrix}\)
Diese lokalen Größen müssen allerdings nun in globale (also nicht mehr auf das Fahrzeugkoordinatensystem bezogen) umgerechnet werden, damit sie mit den Ortsinformationen in der Karte zusammengefügt werden können.
Global
\[\begin{matrix}\dot x = v_x \cdot \cos(\phi) \\ \dot y = v_x \cdot \sin(\phi) \\ \dot \phi_g = \omega \end{matrix}\]
Nun haben wir nämlich die Bescherung: Zur Berechnung der Zustandsübergangsmatrix (Dynamikmatrix) sind Winkelfunktionen notwendig, zum anderen ist in den Zuständen die Fahrtrichtung φ mit enthalten, welche ja selbst ein Zustand darstellt.
Nichtlineare Zustandsüberführung
Der Trick, welcher beim Extended Kalman Filter gemacht wird, ist folgender: Es wird um den aktuellen Mittelwert und die aktuelle Kovarianz linearisiert! Genauer gesagt: Es wird eine Taylor-Approximation vorgenommen, welche nach dem ersten Glied abgebrochen wird. Hört sich kompliziert an, ist es auch. Visualisiert sieht das so aus:
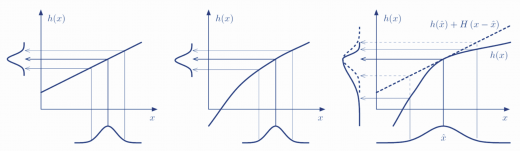
Links: Linearer Zusammenhang führt zu normalverteilter Abbildung. Mitte: Nichtlinearer Zusammenhang führt zu nicht mehr normalverteilter Abbildung, somit ist Kalman Filter nicht mehr anwendbar. Rechts: Linearisierung um aktuellen Zustand führt wieder zu normalverteilter Abbildung. Quelle: Solá – Simultaneaous localization and mapping with the extended Kalman Filter
Beim Kalman Filter war die Zustandsüberführung von x zu x+1 noch durch eine lineare Matrix realisiert. Das geht nun so nicht mehr. Beim EKF wird der Zustandsübergang durch eine Gleichung (z.B. sin(x)) realisiert. Dafür muss diese aber, um die Linearisierung zu erreichen, am aktuellen Zustand differenziert (Anstieg berechnen) und mit einer kleinen Schrittweite multipliziert werden.
\[x_\text{t+1} = x_t + \frac{\partial f}{\partial x}\cdot (x-\overline x)\]
Das sieht kompliziert aus, sagt aber nur, dass man die Funktion an der Stelle an der sie sich befindet partiell ableitet und mit einem kleinen Rechenschritt multipliziert.
Unterschied Kalman Filter und Extended Kalman Filter

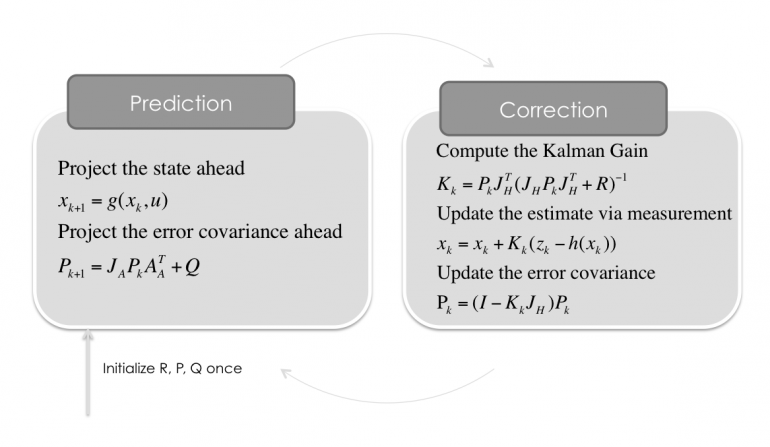
Unterschied zwischen Kalman Filter und Erweitertes Kalman Filter: Die Zustandsüberführung wird durch eine Gleichung beschrieben statt einer Matrix und die Kovarianzmatrix wird mit den partiellen Ableitungen (Jacobi-Matrix) berechnet. Das selbe bei der Messgleichung im Correct Schritt.
Fahrzeug als Systemmodell
Das vorher genannte Systemmodell wird nun noch um ein paar Zustände erweitert, da dies eine bessere Beschreibung des realen Fahrzeugmodells ermöglicht. Das nachfolgende Sytemmodell wird auch als “Constant Turn Rate and Velocity” (kurz: CTRV Modell) bezeichnet, weil es von einer Bewegung mit konstanter Geschwindigkeit und konstantem Kurvenradius ausgeht. Eine gute Approximation für ein Fahrzeug auf einer Straße kann mit der Position in x, Position in y, Fahrtrichtung φ, Geschwindigkeit in Fahrtrichtung v sowie der Drehrate um die Hochachse (Gierrate) ω beschrieben werden. Der Zustandsvektor ist dann:
\[x_\text{CTRV}= \begin{bmatrix}
x \\ y \\ \phi \\ v_x \\ \omega
\end{bmatrix}\]
Die für das Kalman Filter benötigte Gleichung, welche den Zusammenhang der Systemzustände beschreibt, kann über die Drehung des Fahrzeugs in der komplexen Ebene hergeleitet werden (Danke Willy!).
\[g_A=\begin{bmatrix}
\frac{v}{\omega}\left(\sin(\omega T+\phi)-\sin(\phi)\right)+x \\
\frac{v}{\omega}\left(-\cos(\omega T+\phi)+\cos(\phi)\right)+y \\
\omega T + \phi \\
v_x \\
\omega
\end{bmatrix}\]
Diese Zusammenhänge müssten jetzt in Matrixform gebracht und partiell abgeleitet werden. Tatsächlich kann man aber ausnutzen, dass man es ohnehin mit einem PC oder Mikrocontroller berechnen möchte und ohnehin nur eine endliche Rechenschrittweite erreicht. Eine numerische Lösung des Problems bietet sich an!
Numerische Berechnung der partiellen Ableitungen
Die Bildung der benötigten Jacobi-Matrix kann über bekannte Verfahren der numerischen Mathematik vorgenommen werden. Beispielhaft über den Vorwärtsdifferenzenquotienten statt des partiellen Differentials.
\[\frac{\partial F}{\partial x_k}\approx \Delta F(x)=\frac{1}{h}\cdot\left(F(x+he_k)-F(x)\right)\]
Zurück zum Beispiel
Die vom CTRV Modell messbaren Zustände (im Tunnel) sind nur die letzten beiden, d.h. die Geschwindigkeit in Fahrzeuglängsrichtung und die Drehrate. Benötigt wird aber die globale Position x und y, denn damit kann ja berechnet werden, wo sich das Fahrzeug befindet.
Extended Kalman Filter in Matlab
Die Implementierung des EKF wurde dem Beispiel “Learning the Extended Kalman Filter” von Yi Cao entnommen. Dabei wurde das Modell mit einer Abtastrate von 20ms (Fahrzeug-CAN üblich) berechnet. Initialisiert wurde es mit 130km/h in x-Richtung und einer Drehrate von 0.01rad/s.
%% Extended Kalman Filter Beispiel
% Quelle: <http://www.mathworks.com/matlabcentral/fileexchange/18189-learning-the-extended-kalman-filter>
%
clear all; close all; clc;
n=5; %number of states
q=0.001; %std of process
r=0.01; %std of measurement
Q=q^2*eye(n); % covariance of process
R=r^2; % covariance of measurement
T=0.02; % Timestep
%% Fahrzeugmodell CTRV
% Constant Turn Rate and Velocity
%
% $$ x= \left [ \matrix{ x\cr
% y\cr
% \phi\cr
% v\cr
% \omega}\right]$$
%
% Dieses Modell wird aus der Drehung des Fahrzeugs auf einem Kreisbogen
% auf Grundlage der physikalischen Randbedingungen erzeugt. Hilfe: Drehung
% über komplexe Zahlen herleiten!
%
% Mehr dazu: <http://www.qucosa.de/fileadmin/data/qucosa/documents/5874/data/Diplomarbeit.pdf>
%
f=@(x)[(x(4)/x(5))*sin(x(5)*T+x(3)) - (x(4)/x(5))*sin(x(3))+x(1);...
-(x(4)/x(5))*cos(x(5)*T+x(3)) + (x(4)/x(5))*cos(x(3))+x(2);...
x(5)*T+x(3);...
x(4);...
x(5)]; % nonlinear state equations
%% Measurement
% Üblich im Fahrzeug: Geschwindigkeit und Gierrate messbar
%
h=@(x)[x(4); x(5)]; % measurement equation
%% Initialisierung
%
s=[0; 0; 0; 130/3.6; 0.01]; % initial state
x=s+q*randn(n,1); %initial state % initial state with noise
P = eye(n); % initial state covariance
N=500; % total dynamic steps
xV = zeros(n,N); %estmate % allocate memory
sV = zeros(n,N); %actual
zV = zeros(2,N);
%% Extended Kalman Filter
% Hier werden die Filterdurchläufe (Update / Predict) abgearbeitet
%
for k=1:N
z = h(s)+[r; 0.01*r]*randn; % measurments
sV(:,k)= s; % save actual state
zV(:,k) = z; % save measurment
[x, P] = ekf(f,x,P,h,z,Q,R); % ekf
xV(:,k) = x; % save estimate
s = f(s) + q*randn(n,1); % update process
end
Der Kern der Sache ist die Funktion [x,P]=ekf(f,x,P,h,z,Q,R), welche die eigentliche Zustandsschätzung ausführt. Diese Funktion kann dem Beispiel Beispiel “Learning the Extended Kalman Filter” von Yi Cao entnommen werden.
function [x,P]=ekf(fstate,x,P,hmeas,z,Q,R)
% EKF Extended Kalman Filter for nonlinear dynamic systems
% [x, P] = ekf(f,x,P,h,z,Q,R) returns state estimate, x and state covariance, P
% for nonlinear dynamic system:
% x_k+1 = f(x_k) + w_k
% z_k = h(x_k) + v_k
% where w ~ N(0,Q) meaning w is gaussian noise with covariance Q
% v ~ N(0,R) meaning v is gaussian noise with covariance R
% Inputs: f: function handle for f(x)
% x: "a priori" state estimate
% P: "a priori" estimated state covariance
% h: fanction handle for h(x)
% z: current measurement
% Q: process noise covariance
% R: measurement noise covariance
% Output: x: "a posteriori" state estimate
% P: "a posteriori" state covariance
[x1,A]=jaccsd(fstate,x); %nonlinear update and linearization at current state
P=A*P*A'+Q; %partial update
[z1,H]=jaccsd(hmeas,x1); %nonlinear measurement and linearization
P12=P*H'; %cross covariance
% K=P12*inv(H*P12+R); %Kalman filter gain
% x=x1+K*(z-z1); %state estimate
% P=P-K*P12'; %state covariance matrix
R=chol(H*P12+R); %Cholesky factorization
U=P12/R; %K=U/R'; Faster because of back substitution
x=x1+U*(R'\(z-z1)); %Back substitution to get state update
P=P-U*U'; %Covariance update, U*U'=P12/R/R'*P12'=K*P12.
function [z,A]=jaccsd(fun,x)
% JACCSD Jacobian through complex step differentiation
% [z J] = jaccsd(f,x)
% z = f(x)
% J = f'(x)
%
z=fun(x);
n=numel(x);
m=numel(z);
A=zeros(m,n);
h=n*eps;
for k=1:n
x1=x;
x1(k)=x1(k)+h*i;
A(:,k)=imag(fun(x1))/h;
end
Zu erkennen ist, dass eine andere Art der numerischen Berechnung der Jacobi-Matrix genutzt wurde. Außerdem die Cholesky Zerlegung und eine Substitution. Dies sind alles Optimierungen für eine effizientere Berechnung.
Interessanter ist das Resultat!
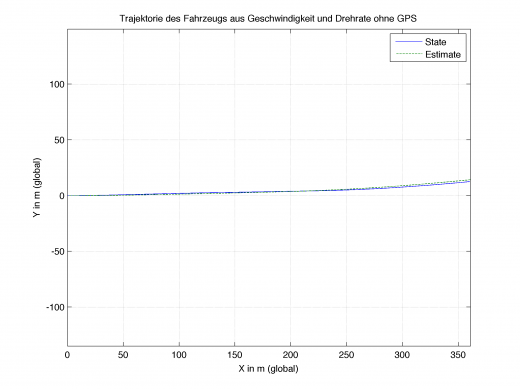
Schätzung der Fahrzeugposition nur mit Geschwindigkeit und Drehrate mit Hilfe des Extended Kalman Filters
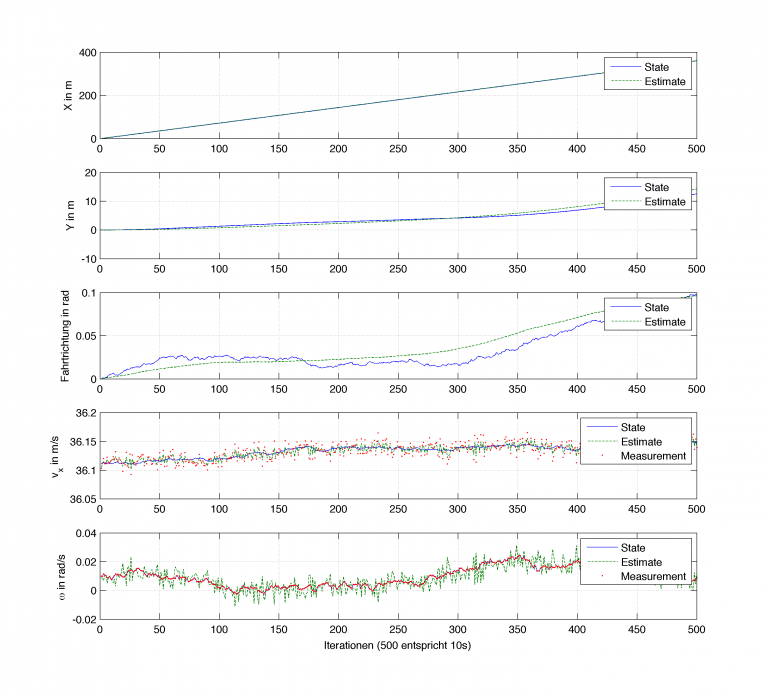
Die 5 Zustände des CTRV Zustandsvektors dargestellt. Zu sehen: Nur die unteren beiden (Geschwindigkeit und Drehrate) wurden auch durch Messungen gestützt, die anderen sind lediglich durch das EKF berechnet.
Die Trajektorie des Fahrzeugs sieht nachfolgend aus.
Das sieht natürlich sehr sehr gut aus! Das Filter ist in der Lage die Position des Fahrzeugs zu berechnen, obwohl keine Positionsinformationen mehr vom GPS kommen. Hier dargestellt sind lediglich 10s, das Ergebnis wird mit zunehmender Zeit natürlich immer ungenauer, klar.
Python Implementierung des Extended Kalman Filters
Extended Kalman Filter with CTRV Vehicle Model in Python from Paul Balzer on Vimeo.
Das IPython Notebook aus dem Video ist auf http://balzer82.github.io/Kalman/ zu finden.
Ach übrigens: Für kommerzielle Anfragen gibt es auch die Möglichkeit mich zum Thema zu konsultieren: Hire me!






36 Comments
Hallo Herr Balzer,
ihr Blog hat mir schon sehr geholfen das (erweiterte) Kalmanfilter zu verstehen. Aber könnten sie in der Tabelle, die das Kalmanfilter und das erweiterte Kalmanfilter vergleichend darstellt, die Formelzeichen an die aus ihrem Artikel zum 2-D-Kalmanfilter anpassen oder nochmal eine Legende zu den Formeln erstellen? Denn in dem Artikel zum 2-D-Kalman ist weder ein A noch ein Q oder C als Variablen verzeichnet.
Herzlichen Dank,
Mathias Artus
Könnte es ein, dass im Teil “Unterschied Kalman Filter und Extended Kalman Filter” Predict und Update vertauscht wurden?
Die Messung kommt sollte im Update Schritt einbezogen werden. Im Predict Schritt wird – in diesem Beispiel – nur Geschwindigkeit*Zeit auf die Position addiert und das tut ja die Funktion g_A (bzw. im KF die Matrix A).
Hallo Niklas, ich glaube du hast Recht, das habe ich vertauscht! Hab die Grafik aktualisiert. Danke
Ich bin beim Implementieren meines eigenen Extended Kalman Filters im hier aufgeführten Matlab Code über die Definition der Messfunktion h gestolpert und habe einige Zeit versucht zu verstehen warum diese so gewählt wurde.
Zur Erklärung:
Die Messdaten werden aus dem State des Filters genommen und ein Rauschen draufaddiert um reale Messdaten zu simulieren.
Hätte man reale, externe Messdaten, würde man in der Messfunktion in diesem hier vorgestellten Bsp einen Null-Vektor zurückgeben (keine Abhängigkeit vom State) und stattdessen in der Zeile wo z gesetzt wird (direkt nach dem for) die Messdaten setzen:
z = messdaten(:,k)
Ganz sicher bin ich mir an der Stelle jedoch nicht.
Hallo Martin,
schau dir mal die Videos vom Prof. Klaus Brenner an, der erklärt das sehr ausführlich, damit müssten alle Fragen geklärt sein. :)
http://www.youtube.com/watch?v=U2fE1AkmGmg&list=PLpUPoM7Rgzi_7YWn14Va2FODh7LzADBSm
Ich habe es natürlich so vereinfacht, dass man es verstehen kann. Hier soll ein Einstieg in die Thematik gebracht werden, ich habe viele Sachen weg gelassen.
Grüße
Hallo Martin,
ich habe den Artikel noch mal etwas überarbeitet, weil ich die Matlab Lösung nicht so schön finde. Die ist in der Tat verwirrend, weil dort numerisch differenziert wird und auch mit den Funktionen hin & her gesprungen wird.
Schau dir mal das eingebettete Video an mit der Python Implementierung, dann wird es deutlicher hoffe ich!
Grüße
Hallo,
da ich nirgendwo nachfragen kann, hoffe ich hier auf eine kleine Unterstützung und Hilfe.
Ich soll ein Kalman Filter schreiben, welcher die Position des Robots glättet.
Dafür bekomme ich lediglich die Position (X,Y) in jedem Schritt.
Wenn ich eine Systemgleichung der Art: X(t) = X(t-1) + V(t-1) * dT,
Mein Zustandsvektor wäre [X,Y,Vx,Vy] muss ich dann die EKF benutzen?
Ist es überhaupt sinnvoll, solche Systemgleichung zu benutzen, da V(t) oder a(t) ja von delta X bzw. delta Y abgeleitet werden.
Ich würde mich über die Hilfe sehr sehr freuen.
Schöne Grüße, Vince
Hallo Vince,
für den von dir angesprochenen Systemzustand benötigst du keinen Extended Kalman Filter. Ein einfacher, wie in https://www.cbcity.de/das-kalman-filter-einfach-erklaert-teil-2 erläutert reicht. Da ist sogar das Systemmodell, was du benötigst direkt genutzt worden.
Viel Erfolg!
Hallo Paul,
auch ich hab da mal ein paar Fragen, vielleicht mache ich ja auch etwas grundsätzliches falsch.
Zuerst aber einmal ein großes Lob, das ist wirklich gut gelungen und leicht verständlich in der Tat.
Aber ich verstehe es noch nicht wie ich das anstelle, wenn ich in Echtzeit die Messwerte verarbeiten möchte. Das Pythonskript habe ich mir angeschaut, aber leider bin ich damit nicht so sehr vertraut, ein Matlabskript hast du nicht zufällig, oder eine empfehlung wo man das ebenso einfach nachlesen kann?
x_k = [x_km1(4);
x_km1(5);
x_km1(6);
u1;
u2;
-(2*x_km1(5)*x_km1(6)+g*sin(x_km1(3))-u1*cos(x_km1(3)))/(x_km1(2))];
ist meine Zustandsgleichung und ich würde gern dafür ein EKF entwerfen. Dabei bin ich glaub ich etwas auf dem Holzweg und wäre über jeden Tipp erfreut.
Viele Grüße
Marcel
Auch von mir vielen Dank für diese tolle Zusammenfassung! :-)
Obwohl ich auch nicht ganz verstehe wie man auf das Systemmodell kommt, aber da gibt es vermutlich auch genug Beiträge.
Ich war außerdem etwas verwundert, dass der MatLabcode beim Ausführen keine Ergebnisse anzeigt. Der Blick in die Originalsourcen hat offenbart, dass hier der Plot (bewusst?) weggelassen wurde..
Hallo Baer,
ja, wie man auf diese Systemmodelle kommt, wird wohl immer ein Geheimnis der Physiker und Maschinendynamiker bleiben… :)
Aber dafür gibt es zum Glück Bücher, wo die gängigsten so drin stehen. Viel interessanter ist die Wahl der Q und P Matrix, da widersprechen sich die Literaturquellen auch alle. Das ist also das so genannte Filter-Tuning, wofür es ganze Professuren gibt.
Das stimmt, im Matlab Code ist keine Anweisung zum Erstellen des Plots enthalten.
Stimmt der Satz unter dem Vergleich zwischen Kalman und EKF: “[…]Das selbe bei der Messgleichung im Predict Schritt.”? Sollte es nicht heißen: ” …im Correct Schritt?
Viele Grüße
Das stimmt! Danke, habe es geändert.
Hallo Paul, zunächst mal vielen Dank für deine Mühe, das so detailliert darzustellen! Ich habe selbst Erfahrung mit Schätzung/Kalman-Filter und so weiter und frage mich Folgendes: in deiner zeitdiskreten Dynamik gehst du von konstanter Geschwindigkeit und konstanter Gierrate aus, i.e.
v_{x,k+1} = v_{x,k}
\omega_{k+1} = \omega_{k}
und deinem Matlab-Beispiel zufolge sind diese auch näherungsweise konstant. Für deine Implementierung in Python jedoch, siehe
http://nbviewer.ipython.org/github/balzer82/Kalman/blob/master/Extended-Kalman-Filter-CTRV.ipynb?create=1
verwendest du auch dieses Modell und dort ist die Geschwindigkeit alles andere als konstant.. siehe Plots kurz vor Position x/y. Meine Frage: funktioniert das CRTV-Modell trotzdem, weil du das Prozessrauschen hinreichend groß gewählt hast? Wie sind deine Erfahrungen damit?
Vielen Dank für deine Antwort!
Hallo Tillmann,
die Aussage, dass es konstant ist, bezieht sich nur darauf, dass es innerhalb einer Rechenschrittweite (delta T) keine großen Änderungen gibt.
Am Beispiel der Längsgeschwindigkeit: Nehmen wir mal ein Auto, was von 0…100km/h in 5s beschleunigt. Das ist schon sportlich. Die Beschleunigung ist 5,5m/s2. Wenn du das Kalman Filter mit einer Rechenschrittweite von dt=0,02s rechnest, dann ändert sich die Geschwindigkeit von dem Auto innerhalb dieser 0,02s um 0,11m/s. Das ist zwar nicht 0m/s (was konstant wäre), aber auch nicht sooo viel.
Solltest du einen Prozess filtern wollen, der sich schneller ändert oder wenn du die Rechenschrittweite nicht so klein wählen kannst, dann kannst du auch noch eine Dimension höher gehen und das CTRA Dynamikmodell (Contant Turnrate, Constant Acceleration) wählen. Da ist innerhalb einer Rechenschrittweite die Beschleunigung konstant, was im Beispiel des Autos ja dann so wäre (nämlich 5,5m/s2).
Wenn du die Process Noise Covariance Matrix aber so gestaltest, dass eine Abweichung von der idealen Annahme möglich ist, dann konvergiert das Filter auch mit dem CTRV und alles ist gut.
Hallo Paul, genau das waren meine Überlegungen: kleine Änderungen der Geschwindigkeit lässt du mithilfe der Matrix für das Prozessrauschen zu. Dein zeitdiskretes Modell für Geschwindigkeit und Gierrate sind
v_{x,k+1} = v_{x,k} + w_{k,1}
\omega_{k+1} = \omega_{k} + w_{k,2},
wobei w_{k,1} und w_{k,2} je zero-mean Gaussian white noise darstellen, welche ein gewisses ‘Rauschen’ von Geschwindigkeit und Gierrate modellieren.
Klar — wenn es die Anwendung zulässt, z.B. Fahrt auf einer Autobahn, und das Modell hinreichend gut zu sein scheint, dann spricht nichts dagegen, diesen Ansatz zu wählen.
Thumbs up :)
Hey Paul,
vielen Dank, klasse Beitrag.
Wenn es darum geht, die Lage im Raum bzgl. der Winkel zu identifizieren, wie wäre dann mein Zustandsvektor?
Ich habe 3-Achs Gyros und 3-Achs Acc´s zur Verfügung.
x=[ax ay az rx ry rz]
passt das, oder muss ich die Winkel, die ich später mal wissen will, in diesen Vektor mit einbeziehen?
Vielen Dank und viele Grüße
Ben
Hm. Irgendwie schon. Wo willst du den Wert sonst her nehmen, wenn er nicht im Zustandsvektor mit berechnet wird.
Wenn du die Lage einer 6DoF IMU im Raum berechnen willst, dann gehen die üblichen Algorithmen davon aus, dass die Erdbeschleunigung (in Ruhe) die einzige ist und dann wird die “Richtung nach unten” berechnet. Damit weißt du aber immer noch nicht, in welche Richtung in der Horizontalen die IMU zeigt. Dafür brauchst du eine 9DoF IMU (mit Magnetsensor) oder du kannst eben nur die Drehraten aufintegrieren und das wird dann ungenau mit zunehmender Zeit.
Falls du es einfach nur gelöst haben willst (und nicht zum lernen mal selbst machen willst), würde ich dir empfehlen die Tinkerforge IMU 2.0 zu kaufen, die Jungs haben das gut gemacht!
Hallo,
erstmal danke für die hilfreichen Erklärungen. Kurze Frage um erweiterten Modell (CTRV), ich benötige den Fall der Positionsschätzung im Tunnel, wenn keine bzw. nur noch unsichere GPS-Lokalisierungen möglich sind.
Dann würde ich die Position gerne weiter schätzen, zum Beispiel eben auf Basis des ESP Geschwindigkeitssignal und der Gierrate, die ebenfalls vom ESP kommt.
Ich habe dies mal versucht zu simulieren, indem ich einfach die ersten GPS Werte noch eingelesen habe aber dann im Weiteren den Filter mit latitude = 0 und longitude = 0 gefüttert habe.
Da kommen jedoch völlig unbrauchbare Positionsschätzwerte heraus. Wenn ich immer 0 eingebe, so passt die Schätzung ganz gut, allerdings natürlich nicht Positionstreu. Hier hatte ich versucht nur die erste GPS-Koordinate einzuspeisen und dann basierend auf dieser weiter ohne GPS (genullt) zu schätzen, was allerdings nicht funktioniert hatte. Hätten Sie hier eine Idee?
Vielen Dank und Gruß
Hallo Christian,
wenn du die GPS Position einfach auf 0.0/0.0 setzt, dann sagst du dem Kalman Filter, dass es die Position bitte auf’s Meer verschieben soll (siehe: https://www.google.de/maps/@0.0,0.0,6z), denn Lat/Lon von 0.0/0.0 ist ja auch eine Position auf der Welt, nämlich da wo sich Nullmeridian und Äquator schneiden.
Wenn du dem Filter sagen willst, dass du keine GPS Position hast, dann musst du das im Correction Schritt in der Measurement Matrix JH machen. Siehe `if GPS[filterstep]:` auf https://github.com/balzer82/Kalman/blob/master/Extended-Kalman-Filter-CTRV.ipynb?create=1
Da unterscheidet sich die Mess-Matrix dahingehend, dass du wenn GPS vorhanden ist die Positionszustände aktualisierst, wenn keine GPS Position vorhanden ist, schreibst du eine 0 in die Mess-Matrix und der Zustand wird nicht aktualisiert vom Correction-Step. Natürlich integrierst du damit die Messfehler von Geschwindigkeits- und Gierratensensor auf. Je nachdem wie gut die sind, wirst du nach ein paar Sekunden/Minuten relevante Fehler in der Positionsschätzung haben.
Hilft dir das?
Hallo Paul,
danke für deine Antwort. Das ist soweit klar!
Jetzt habe ich noch eine Frage, ich möchte die Rechenschrittweite verändern, d.h. dass die Messwerte der Sensoren (Gierrate, Geschwindigkeit) alle 100 ms kommen und die GPS-Position alle 1s einmal.
Ich habe mal die Messdaten adaptiert, sodass ich z.B. nur jeden 5 Messwert und jeden 50 GPS Wert verwende (um die 50Hz down zu samplen).
Nun bekomme ich jedoch “stufige” Verläufe, die der EKF berechnet.
Würde das so noch funktionieren, ggf. durch Adaption der Process Noise Covariance Matrix Q? Wenn ja wie müsste die dann aussehen? Oder bräuchte ich hierbei ein anderes Modell?
Kann der EKF eigentlich “asynchron” getriggert werden oder müssen die Daten von GPS und Sensoren “aligned” werden (Interpolation der GPS-Werte?).
Danke und viele Grüße
Hallo Christian,
das ist eigentlich die gleiche Frage. Du lässt das Filter mit dt=100ms laufen. Wenn ein GPS Signal alle 1s kommt, dann setzt du in der Messmatrix H den Wert für GPS auf 1, sonst lässt du ihn 0.
Das ist übrigens exakt der Fall, den ich dir verlinkt habe (https://github.com/balzer82/Kalman/blob/master/Extended-Kalman-Filter-CTRV.ipynb?create=1).
Da läuft das Filter mit 50Hz und GPS mit 1Hz.
Was mir noch einfällt: Wenn du mit einem Sensor/Messung direkt einen Wert im Zustandsvektor (z.B. die Position) updatest, dann kann die natürlich ‘springen’.
Umso kleiner der Wert in Q (Varianz des Prozessrauschens) im Vergleich zum entsprechenden Wert in R ist (Varianz des Messrauschens), umso weniger wird es sich durch die Messung beeinflussen lassen und springen. Allerdings ist dann dein Prozess auch träger, d.h. in Kurven o.ä. wird er nicht hinterher kommen.
Hier ein Tracking, wo du den Unterschied zwischen 50Hz und 1Hz siehst: http://mechlab-engineering.de/wordpress/wp-content/uploads/2014/03/Extended-Kalman-Filter-CTRV-Adaptive-Trajectory.png
Danke für deine Ausführungen! Ich werde mal aufgrund der langsameren Sample-Rates des Prozesses das CTRA Dynamikmodell ausprobieren.
Finde hierzu allerdings nicht allzu viele Infos, hättest du hier ein paar Quellen für mich?
Was muss ich tun wenn keine Messung vorhanden ist? Nehme ich dann nur das Kinematikmodell (also nur x=gA(x,u))? oder muss ich auch immer die Covariance Pt mitberechnen?
Die Kovarianz-Matrix P muss in jedem Fall mit berechnet werden. Denn wenn du keine Messung hast, wird die im ‘Prediction’ Step immer größer und größer (es kommt ja +Q dazu) und das zeigt dem Filter, dass es immer weniger sicher ist. Du hast ja keine Messungen.
Wenn du keine hast, kannst du den Correction Step einfach weg lassen (man sagt das Filter läuft ‘Open Loop’) oder du setzt die Messfunktion `h` auf Nullvektor (0).
Was muss ich tun wenn keine Messung vorhanden ist? Nehme ich dann nur das Kinematikmodell (also nur x=gA(x,u))? oder muss ich auch immer die Covariance Pt mitberechnen?
Hallo Paul,
danke für die interessanten Ausführungen. Ich habe eine Frage zum Matlab Skript.
Im Corrector Schritt wird der neue geschätzte Zustandsvektor zu \(x_{est} = x1 + K \cdot (y – h(x1))\) berechnet.
Wenn ich das richtig nachvollzogen habe, so wird in einem deinem Skript die Messung \(y\) zum Zeitpunkt \(t0\) aufgenommen, aber die Differenz zur “virtuellen” Messung \(h(x1)\) zum Zeitpunkt \(t1\) gebildet. Müsste \(y\) nicht zum Zeitpunkt \(t1\) gemessen werden, konkret statt \(h(s)\), \(h(f(s))\) nehmen ?
Eine andere Frage betrifft die Übergangsmatrix. Üblicherweise habe ich kontinuierliche Modelle in Zustandsnormalform \(x_{dot} = A \cdot x + B \cdot u\), wie kommt man denn von dieser in die diskrete Form der Übergangsmatrix \(x_{t+1} = Phi(t) \cdot x(t)\) ?
Hallo Herr Balzer,
eine schöne Einführung zum Thema haben Sie hier erstellt. Was ich mich bei diesem Part zum EKF Frage ist folgendes:
Die Drehwinkelgeschwindigkeit im letzten Diagramm sieht “extrem” stark verrauscht aus. Die Messpunkte liegen auf den richtigen Statezustand. Kann es sein, dass bei bei der Kovarianz für die Messung anstatt:
R=r^2 ein R=r^2*eye(2,2) gemeint war?
Schönen Gruß
Andreas
Can you provide additional details on the advantages or considerations of using Python for implementing EKF compared to other programming languages, and are there specific libraries or tools that are commonly used in EKF implementations in Python?