Der ein oder andere hat sich vielleicht schon mal gefragt, was am Autoradio die Knöpfe AM und FM bedeuten, kommen doch bei beiden mehr oder weniger gute Radiosender an. Es handelt sich dabei um verschiedene Verfahren, mit welchen die Radiostationen ihre Audiosignale Codieren, um sie über Funk durch die Luft an das Autoradio zu senden.

Diese Codierung ist notwendig, weil Sprache, Musik und unsere Ohren in einem Frequenzbereich von 20…20.000Hz arbeiten. Geht man einige Meter von einem sprechenden Menschen weg, so ist er kaum noch zu verstehen. Die Dämpfung von Audiosignalen in der Luft ist erheblich, in diesem Frequenzbereich kann Radio also nicht übertragen werden. Das Audiosignal muss an der Quelle codiert werden, damit es über weitere Strecken übertragen werden kann. Eines dieser Verfahren, wenn auch ein sehr sehr einfaches, ist die so genannte Amplitudenmodulation AM.
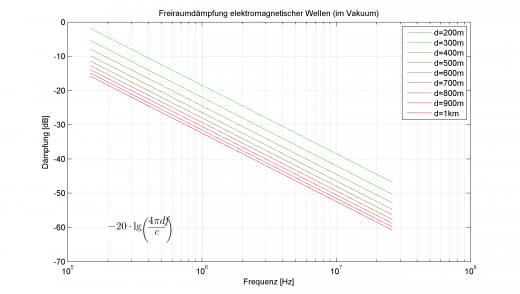
Dämpfung von Signalen in Abhängigkeit ihrer Frequenz
Wie gesagt befindet sich der interessante Bereich, welcher im Radio von Interesse ist, zwischen 20…20.000Hz. Die Dämpfung, welche ein Audiosignal bei der Übertragung durch die Luft erfährt ist immens. Bei 2-facher Entfernung zum Lautsprecher ist der Schalldruckpegel nur noch 1/2 so groß (1/r-Gesetz).
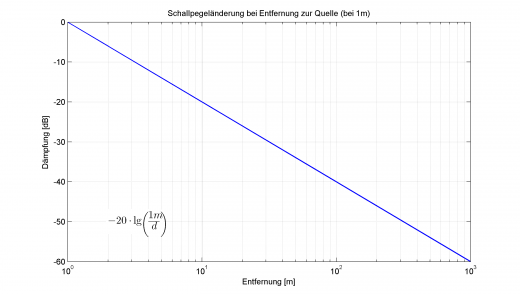
Änderung des Schalldruckpegels für Audiosignale in Abhängigkeit des Abstands von der Schallquelle (logarithmisch!). Dabei entspricht -6db schon einer Halbierung des Schalldruckpegels.
Es ist offensichtlich, dass höchstens im Wohnzimmer, oder bei hoher Schallleistung auch auf Festivalgeländen, eine relevante Entfernung überbrückt werden kann. Für den Einsatz über lange Distanzen, wie es beim Radioempfang notwendig ist, muss der Frequenzbereich 20…20.000Hz verlassen werden.
Geht man mit der Frequenz erheblich höher und nutzt elektromagnetische Wellen, so sieht die Dämpfung schon etwas anders aus.
Bei elektromagnetischen Wellen ist die Dämpfung auch noch von der Frequenz abhängig. Zum Vergleich beider Diagramme sei die Dämpfung bei einer zu überwindenden Entfernung von 1km gewählt: Das Audiosignal hat eine Dämpfung von -60db, eine elektromagnetische Welle mit 200kHz lediglich -18dB, was durch die logarithmische Dekade ungefähr dem Verhältnis 1000/8 entspricht. Also eine erheblich geringere Dämpfung für die elektromagnetische Welle.
Trägerfrequenz
Nachdem nun klar ist, weshalb man lieber mit höherfrequenten elektromagnetischen Wellen über größere Distanzen das Radiosignal übertragen sollte, bleibt weiterhin das Problem, das man ja Audiosignale übertragen möchte.
Dazu gibt es das Verfahren der Modulation. Man prägt einer Grundschwingung einfach eine gewünschte Schwingung auf. In diesem einfachen Fall soll eine Trägerfrequenz von 2000Hz angenommen werden.
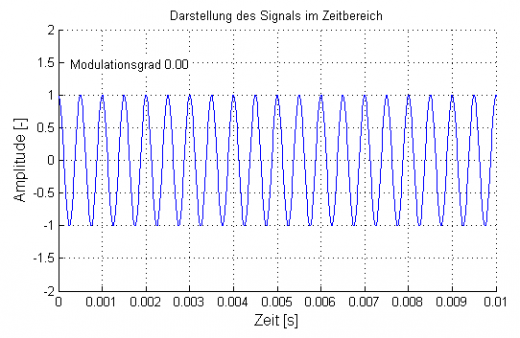
Schwingung mit 2000Hz
Amplitudenmodulation
Auf diese Trägerfrequenz soll nun das gewünschte Audiosignal aufmoduliert werden. Um die Sache einfach darstellen zu können, soll nur ein monotones Brummen mit fmod=200Hz auf die Trägerfrequenz von f=2000Hz aufmoduliert werden.
Wie der Name Amplitudenmodulation schon vermuten lässt, wird die Amplitude der Trägerschwingung verändert.
Das sieht alles komplizierter aus, als es ist. Letztendlich wird nur die Höhe der Amplitude selbst mit der Zeit variiert. Dabei ändert sich die Höhe der Amplituden genau so oft, wie es die aufmodulierte Schwingung vorgibt.
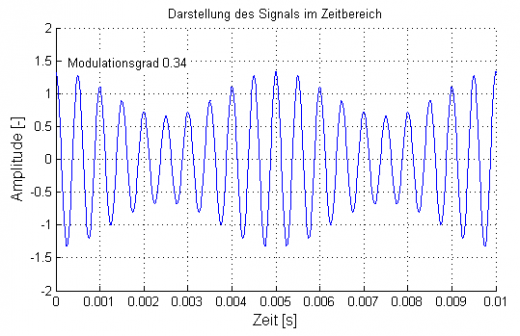
Trägerfrequenz von 2000Hz mit aufmodulierter Frequenz von 200Hz
Dieses Signal kann jetzt im Empfangsgerät (Radio) mit einfachen Bauteilen wieder demoduliert werden und die eigentliche Audioschwingung bleibt übrig.
Frequenzspektrum
Interessant ist auch ein Blick auf das Frequenzspektrum dieser Signale.
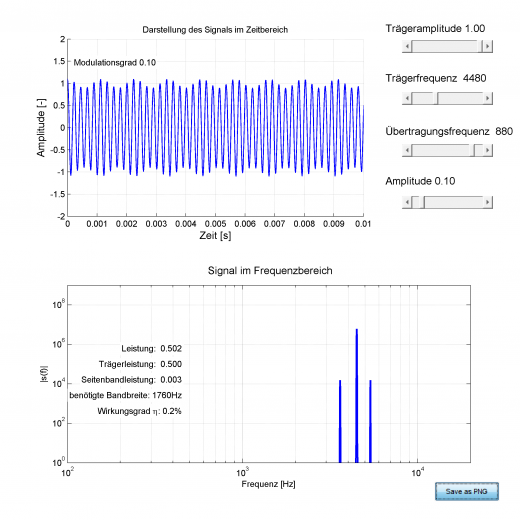
Amplitudenmoduliertes Signal (880Hz) auf Trägerfrequenz (4480Hz) mit dazugehörigem Frequenzspektrum und erkennbaren Seitenbändern (links -880Hz und rechts +880Hz von Trägerfrequenz)
Die Höhe der gewählten Modulationsamplitude Amod ist entscheidend für Leistungen und Wirkungsgrad dieser Übertragungsmethode. Ein Grenzwert im Wirkungsgrad wird bei 17% erreicht. Ein sehr schwaches Ergebnis. Dies, und die hohe Störanfälligkeit, sowie das Fortschreiten der digitalen Technik, haben die Amplitudenmodulation eigentlich als Standard abgelöst. Nur noch im Bereich der LW, MW und KW Analogradios sowie beim analog-TV wird diese Modulationsmethode angewendet.
Matlab Code zum erzeugen der Amplitudenmodulation und Frequenzanalyse
clear all;
close all;
clc;
%% Amplitudenmodulation GUI für Matlab %%%%%%%%%%%%%%%%%
% Paul Balzer
% www.cbcity.de
% unter CC-BY-SA 2.0 Lizenz
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Parameterinitialisierung
A=0; %Signalamplitude
f=0; %Signalfrequenz
f0=1000; %Trägerfrequenz
A0=1.0; %Trägeramplitude
%Zeitbasis
t=linspace(0,0.1,10000);
% Grafik erzeugen
fighandle=figure;
set(gcf,'Position',[100 100 800 800])
set(gcf,'Name','Amplitudenmodulation','Resize','off','Paperpositionmode','auto');
sub(1)=subplot(2,2,1);
title('Darstellung des Signals im Zeitbereich')
p1=get(gca,'Position') ;
zeitaxhandle=gca;
%Formatierung vorab
grid on
signal = line(0,0,'LineWidth',1);
xlabel('Zeit [s]','FontSize',12);
ylabel('Amplitude [-]','FontSize',12);
xlim([0 0.01])
ylim([-2 2])
% Slider erzeugen
sub(2)=subplot(2,2,2);
p2=get(gca,'Position') ;
set(gca,'Position',[p2(1)*1.3 p2(2) p2(3)*0.6 p2(4)])
set(zeitaxhandle,'Position',[p1(1) p1(2) p1(3)*1.7 p1(4)])
axis off
slideraxhandle=gca;
% Amplitude
Aslider = uicontrol('Style', 'slider',...
'Position', [620 480 140 20],'min',0,'max',1,...
'value',0,'String','A');
Atext=text(0,.2,'temp','Fontsize',12);
% Frequenz
fslider = uicontrol('Style', 'slider',...
'Position', [620 560 140 20],'min',1,'max',1000,...
'value',200,'String','f');
ftext=text(0,.48,'temp','Fontsize',12);
% f0
f0slider = uicontrol('Style', 'slider',...
'Position', [620 640 140 20],'min',2000,'max',10000,...
'value',2000,'String','f_0');
f0text=text(0,.78,'temp','Fontsize',12);
% Trägeramplitude
A0slider = uicontrol('Style', 'slider',...
'Position', [620 720 140 20],'min',0,'max',1,...
'value',1,'String','A_0');
A0text=text(0,1.06,'temp','Fontsize',12);
sub(3)=subplot(2,2,3:4);
semilogy(10,1,'LineWidth',2);
% Druckbutton
h = uicontrol('Style', 'pushbutton', 'String', 'Save as PNG',...
'Position', [670 30 100 30], 'Callback',...
'print -dpng -r300 am.png');
% Noch ein Axes drumherum, um alles zu beschriften
ah = axes('position',[0,0,1,1],'visible','off');
ffttitle = text(0.4,0.48,'Signal im Frequenzbereich');
set(ffttitle,'FontSize',12);
mtext = text(0.3,0.88,'temp','Horizontalalign','right','Backgroundcolor',[1 1 1]);
PAMtext= text(0.35,0.33,'temp','Horizontalalign','right','Backgroundcolor',[1 1 1]);
PTrtext= text(0.35,0.3,'temp','Horizontalalign','right','Backgroundcolor',[1 1 1]);
PStext= text(0.35,0.27,'temp','Horizontalalign','right','Backgroundcolor',[1 1 1]);
Btext= text(0.35,0.24,'temp','Horizontalalign','right','Backgroundcolor',[1 1 1]);
etatext= text(0.35,0.21,'temp','Horizontalalign','right','Backgroundcolor',[1 1 1]);
while(ishandle(fighandle))
A = get(Aslider,'value'); % Modulationsamplitude
f = get(fslider,'value'); % Modulationsfrequenz
f0 = get(f0slider,'value'); % Trägerfrequenz
A0 = get(A0slider,'value'); % Trägeramplitude
%% zu übertragendes Signal
w = 2*pi*f;
% Trägerschwingung
w0 = 2*pi*f0;
m = A/A0; %Modulationsgrad
set(mtext,'String',['Modulationsgrad ' num2str(m,'%1.2f')])
%Signal
dA = A*cos(w.*t); %Amplitudenmodulation
s = (A0+dA) .*cos(w0.*t); %Gesamtsignal
%Zeitsignal aktualisieren
set(signal,'xdata',t,'ydata',s);
set(Atext,'string',['Amplitude ' num2str(A,'%1.2f')])
set(ftext,'string',['Übertragungsfrequenz ' num2str(f,'%4.0f')])
set(f0text,'string',['Trägerfrequenz ' num2str(f0,'%4.0f')])
set(A0text,'string',['Trägeramplitude ' num2str(A0,'%1.2f')])
% Leistungen berechnen
R=1; %Normwiderstand
PAM = A0^2/(2*R)*(1+m^2/2);
set(PAMtext,'string',['Leistung: ' num2str(PAM,'%1.3f')])
PTr = A0^2/(2*R); %Trägerleistung
set(PTrtext,'string',['Trägerleistung: ' num2str(PTr,'%1.3f')])
PS = m^2*A0^2/(4*R);%Seitenbandleistung
set(PStext,'string',['Seitenbandleistung: ' num2str(PS,'%1.3f')])
% Bandbreite berechnen
B = 2*f;
set(Btext,'string',['benötigte Bandbreite: ' num2str(B,'%3.0f') 'Hz'])
% Wirkungsgrad berechnen
eta = m^2/(4+2*m^2)*100;
set(etatext,'string',['Wirkungsgrad \eta: ' num2str(eta,'%3.1f') '%'])
%% FFT Berechnen
subplot(sub(3))
% Signal Fenstern um Leakage-Effekt zu vermeiden
antileakage=hann(length(s))';
Y=fft(s.*antileakage); %Frequenzspektrum des Signals berechnen
Y(1)=[]; %erste Zeile ist einfach nur die Summe der Daten
n = length(s);
amplitude = abs(Y(1:floor(n/2))).^2;
nyquist = 1/2;
%x-Achse Bezug herstellen mit Faktoren aus
%Zeitvektor (siehe linspace oben)
freq = (1:n/2)/(n/2)*nyquist*10000/0.1;
loglog(freq,amplitude,'LineWidth',2);
grid on
xlim([100 20000])
ylim([1 10e8])
ylabel('|s(f)|')
xlabel('Frequenz [Hz]')
drawnow
end