Eine oft diskutierte Fragestellung ergibt sich, wenn am Stammtisch die Beschleunigungsfähigkeit zweier PKW (idealerweise von zwei Personen neu erworbene Fahrzeuge) verglichen wird…
Mein neuer Diesel hat 130PS, dein Benziner auch nur 130PS. Diesel PS zählen aber viel mehr als Benziner PS! Egal wieviel PS dein Auto hat, Drehmoment braucht es, und da hat der Diesel viel mehr, merkt man ja auch! Meiner ist schneller.
Stammtische sind ein schwieriger Ort für fachliche Diskussionen, aber trotzdem sei der Versuch gestattet etwas dazu beizutragen…
In einem Verbrennungsmotor wird über die zugeführte Kraftstoffmenge eine Energie freigesetzt, welche den Kolben dazu bewegen, sich vom oberen Totpunkt zu entfernen. Der durch die Explosion entstehende Überdruck im Brennraum ergibt, multipliziert mit der Kolbenfläche, eine Kraft auf das Pleul, welches durch den Hebelarm der Kurbelwelle ein Drehmoment an der Kurbelwelle erzeugt. Mehrere Zylinder bringen mehrere sich überlagernde Drehmomente.
Wird die Kupplung geschlossen, wird das Drehmoment in das Getriebe übertragen, in dem es gewandelt wird. Gewandelt deswegen, weil ein Verbrennungsmotor im Allgemeinen zu wenig Drehmoment hat, um ein Fahrzeug anfahren zu lassen. Das Drehmoment wird durch das Getriebe also erhöht (1. Gang mit Übersetzung z.B. 1:3 erhöht das Drehmoment auf das Dreifache). Allerdings ist das nur die halbe Wahrheit, denn die Leistung vor und nach dem Getriebe ist (abzüglich Verlustleistung) gleich, sodass der Grundsatz
\[\text{Leistung} (W)=\text{Drehmoment} (Nm) \cdot \text{Winkelgeschwindigkeit} (1/s)\]
gilt. Umgerechnet auf gängige Stammtischgrößen gilt:
\[\text{Leistung} (PS) = \text{Drehmoment} (Nm) \cdot \text{Drehzahl} (1/min) \cdot\frac{2\cdot\pi\cdot1.36}{60\cdot1000}\]
Die Getriebeausgangswelle geht dann auf das Differential, in dem das Moment und die Drehzahl nochmal gewandelt wird. Schließlich kommt das Drehmoment stark erhöht am Rad an, wo es über den Radius (Reifenhalbmesser) des Reifens wieder zu einer Kraft wird. Die Zugkraft! Die Drehzahl ergibt über den Reifenradius die Geschwindigkeit die gefahren werden kann.
Jetzt leuchtet es natürlich ein, dass ein A8 mit der Zugkraft eines Smart nicht allzu viel anfangen kann, weil der A8 ja wesentlich schwerer ist. Daher empfiehlt es sich, zum direkten Vergleich zweier Fahrzeuge, die Radzugkraft noch auf die Fahrzeugmasse zu beziehen und in Prozent auszudrücken. Dann ist ein Vergleich der Fahrzeuge ohne Weiteres möglich. Dies stellte Prof. Jante schon 1936 fest.
So, genug Theorie. Jetzt mal zwei Beispiele.
Audi S4 (B5) mit dem 2.7L BiTurbo Motor

- Nennleistung 195kW
- Nennmoment 400Nm
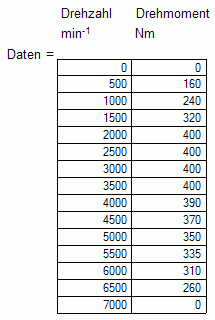
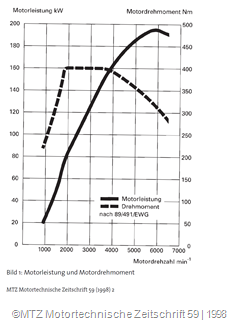
Die für die Berechnung der Zugkraft nötigen Daten wurden einem Audi Prospekt (Übersetzungen, Gesamtmasse) und der Motortechnischen Zeitschrift (MTZ) Ausgabe 1998-02 (Drehmomentkennlinie Motor) entnommen.
Übersetzungen Audi S4 B5 2.7T Quattro
\(i_1=3.500 \\ i_2=1.889 \\ i_3=1.231 \\ i_4=0.967 \\ i_5=0.806\\ i_6=0.684 \\ i_\text{diff}=4.111 \\ m_\text{ges}=1540 kg\)Drehmoment Audi S4 B5 2.7T Quattro
Die Berechnung der Zugkraft und der Geschwindigkeit bei bestimmter Motordrehzahl erfolgt nach folgenden Gleichungen. Der Reifenradius wird auch dynamischer Reifenhalbmesser rdyn genannt. Die Zahlen in den Gleichungen sind zur Umrechnung der Einheiten.
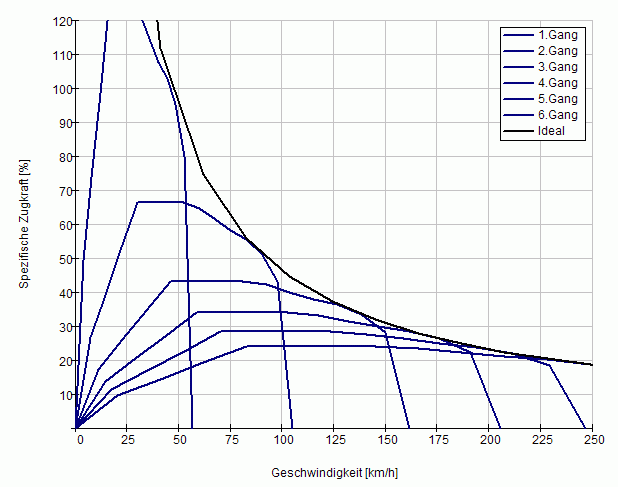
Trägt man die Zugkraft F (normiert auf die Fahrzeugmasse) über der Geschwindigkeit v auf, so ergibt sich für die 6 Gänge:
Zugkraft Audi S4 B5 2.7T Quattro
Anmerkung dazu:
Ersteinmal ist zu sagen, dass das Zugkraftdiagramm als statisches Diagramm zu werten ist. Die Zugkraft ist mit einer Steigungsfähigkeit gleichzusetzen, welche mit dem Fahrzeug überwunden werden kann. Ist damit die Beschleunigung einzuschätzen, müssen Massenträgheiten des Antriebsstrangs mit berücksichtigt werden. Dabei hat ein 6-Zylinder mehr Massenträgheit als ein 4-Zylinder und ein Quattro mehr als ein Fronttriebler. Damit reduziert sich die zur Beschleunigung zur Verfügung stehende Zugkraft. Die Massenträgheitsmomente sind mir aber nicht bekannt, damit kann ich diese nicht mit in die Berechnung einbeziehen.
Was heißt denn nun 100% Zugkraft?
Ganz einfach. 100% der Fahrzeugmasse kann in Zugkraft auf die Straße gebracht werden. Wenn es der Untergrund und die Reifen erlauben, so beschleunigt das Auto bei 100% Zugkraft mit exakt 1g, also der Erdbeschleunigung 9.81m/s². Schön!
Wie man an dem Diagramm erkennt, reicht die Zugkraft des Audi S4 B5 2.7T bis auf über 120%. D.h. wenn die Reifen nicht kleben, wird es wahrscheinlich Rauch an allen 4 Rädern geben, wenn ein B5 S4 startet. Leider spielt gerade in den unteren Gängen die Drehmassenträgheit des Antriebsstranges eine große Rolle, sodass die Zugkraft im 1. und 2. Gang erheblich reduziert wird. Da die Größen (Massenträgheitsmomente etc..) nicht bekannt sind, kann dazu auch keine Berechnung durchgeführt werden. Prof. Mitschke gibt dazu eine Reduzierung um ca. 32% im 1. Gang an.
Audi S4 (B6) mit dem 4.2L Saugmotor

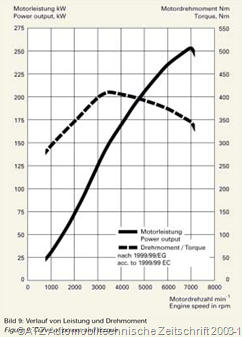
- Nennleistung 253kW
- Nennmoment 410Nm
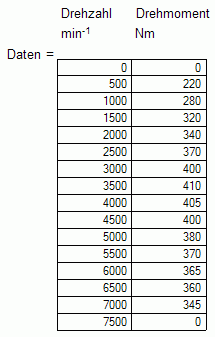
Die für die Berechnung der Zugkraft nötigen Daten wurden einem Audi Prospekt (Übersetzungen, Gesamtmasse) und der Automobiltechnischen Zeitschrift (ATZ) Ausgabe 2003-01 (Drehmomentkennlinie Motor) entnommen.
Die Berechnung erfolgt analog mit folgenden Werten:
Übersetzung Audi S4 B6 4.2 Quattro:
Drehmoment Audi S4 B6 4.2 Quattro:
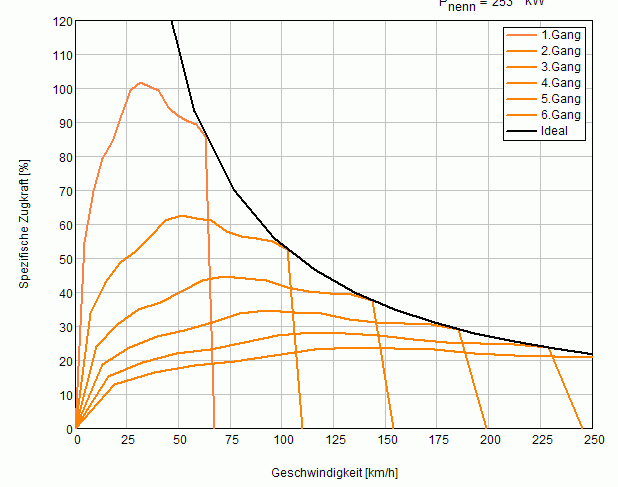
Die Zugkraft ergibt sich dann zu:
Zugkraft Audi S4 B6 4.2 Quattro
Wie zu erkennen ist, gibt es kein homogenes Drehmomentplateau wie es für Turbomotoren üblich ist. Dafür ist das nutzbare Drehzahlband größer.
Ein paar Anmerkungen
Man merkt schon, dass die Diskussion der “besseren” Beschleunigung nicht in ein paar subjektiven Eindrücken fassbar ist. Auch die Meinung vom Stammtischnachbarn, der “letztens einen 3.0L Diesel gefahren ist, und der eine übelste Beschleunigung hatte” sagt nichts aus.
Subjektivität ist generell ein großes Problem, wenn man diese Dinge versucht, miteinander zu vergleichen!
Allein schon die Erwartungshaltung des Fahrers schlägt sich in der subjektiven Wahrnehmung nieder. Ist man dann auch nur Beifahrer, so wirkt die Beschleunigungsänderung wesentlich größer als wenn man selbst fährt.
Als Beispiel sei mal die Straßenbahn angemerkt, in der es schon des öfteren nervt, wenn der Fahrer eine abrubte Beschleunigungsänderung (Ruck) vornimmt und man selbst nicht darauf gefasst war. Der Turbomotor hat eine charakteristische Drehmomentenkennlinie, welche relativ stark ansteigt. Dieser starke Anstieg ist umgerechnet dann der Ruck, welcher auf die Insassen wirkt. Logisch, dass dies als starke Beschleunigung wahrgenommen wird.
Abschließend bleibt zu sagen: Nur Versuch macht klug!





15 Comments
Der Satz “und zu wenig Drehzahl um damit auf die Autobahn zu fahren.” stimmt doch nicht, oder?
bei 200 km/h und bei einem Abrollradius von 1,8 m drehen sich die Räder doch mit 1852 U/min. (Motor ca. 600 U/min)
LG (sonst toller Beitrag!!!)
Hallo Peter. Bei 200km/h und einem Abrollumfang von 1.8m hat man in der Tat die von dir genannte Raddrehzahl. Wie du dann auf 600U/min Motordrehzahl kommst, ist mir nicht klar.
Ich weiß aber was du meinst und hab den Satz raus genommen.
Vorerst mal eine Idee von, die sicher nicht neu ist, jedoch nur selten diskutiert wird. Es geht um die, zumindest für mich, viel zu wenig aussagekräftige Angabe der Spitzenleistung. Denn daraus resultiert das Problem mit den sogenannten Diesel- Turbo- und SaugerPS. Mein Vorschlag zur Abhilfe:
Man nimmt das Drehzahlband von Maximaldrehzahl (oder Drehzahl bei Maximalleistung) bis zur Drehzahl, die vorliegt, schaltet man in den nächst höheren Gang (da auch das von Gang zu Gang variiert, kann man auch hier wieder mitteln). Über dieses Drehzahlband wird die mittlere Leistung und das mttlere Drehmomant bestimmt. Ich denke, dass so viele “Kuriositäten” gar keine mehr wären.
Gruß
Ein wenig aus der Praxis:
Grund des nachfolgenden Schriebs war ein Beschleunigungsrennen von ca.100 auf ca. 230 zwischen meinem e36 M3 3.2l gegen einen e92 335d mit Chip und ca. 340PS, welches ich mit ungefähr 2 Wagenlängen gewann. Der ungläubige Paul (^^) fand dann folgendes im Netz http://www.youtube.com/watch?v=KSwVGkjbshQ&feature=relmfu
Mein Kommentar:
Das ist immer nicht ganz so leicht und, da du das ja gerade leidenschaftlich betreibst ^^, vor ellem nicht immer aus Diagrammen ablesbar! Zum Beispiel hatte mein Gegner 19″ Felgen drauf und ich 17″. In vielen Zeitschriften liest man, dass trotz Leistungssteigerung die originalen Beschleunigungswerte und die Endgeschwindigkeit nicht mehr erreicht werden. Abhilfe schafft immer das montieren der originalen Reifen und Felgen. Es sind rotierende Massen, die eben zum rotieren gebracht werden müssen. Und wenn das Felgenbett weiter außen liegt, muss man eben mehr Energie dafür aufbringen. Aufm Lausitzring kostete einem 5er e34-Fahrer mit ca. 400PS der Umstieg von 17″ auf 18″ 2 Sekunden. Ein komplett auf Renn getrimmtes e36 M3 Coupe braucht knapp 50PS mehr, wenn man von 17 auf 18 Zoll geht und die gleichen Zeiten fahren will. Also, es reicht nicht allein die Leistung oder das Drehmoment zu betrachten. Viele weitere Faktoren spielen noch mit rein.
Da hast du völlig Recht!
Allerdings schreibt der Autor in seiner Anmerkung unter dem ersten F-v-Diagramm, dass er Massenträgheitsmomente im Antriebsstrang nicht kennt und daher nicht berücksichtigt.
Mal angenommen beide Fahrzeuge hätten die gleiche Konfiguration, so könnte man zumind. ein Verhältnis abschätzen.
schöne seite herr kollege, aber schau dir das bitte noch mal an:
Zugkraft Audi S4 B6 4.2 Quattro
“Wie zu erkennen ist, gibt es kein homogenes Drehmomentplateau wie es für Turbomotoren üblich ist. Dafür ist das nutzbare Drehzahlbahn größer.” ?????
der 4.2 ist aber ein sauger!
grüße
p.s. der drehzahlbahn fehlt noch das d :-)
Hallo Schamane,
das Wort “kein” in dem Satz hat ja genau den Zweck das auszudrücken, dass der 4.2 Sauger eben nicht dieses Plateau hat.
Das d habe ich angehangen. Danke
@schamane:
Das passt doch wie es geschrieben wurde!
Der 4.2er ist ein Saugmotor und hat aus diesem Grund kein homogenes Drehmomentenplateau. (Sieht man ja auch im Diagramm…)
Der RS5 hat aber auch ein Drehmomentplateu zwischen 4-6000 wenn ich mich nicht irre. Zum Max. Beschleunigen ist aber die anliegende Höchstleistung in den höheren Drehzahlbereichen am wichtigsten ( ich würde sagen dem oberen Drittel). Die liegt bei diesen Audi Hochdrehzahlsaugern immer recht spät an(glaube sogut wie an der Höchstdrehzahl), das ist an sich nicht so gut.
Eine Frage noch dazu: Gehe ich recht in der Annahme, dass wenn man bei einem Motorrad die Übersetzung i1 durch die Ritzel verändert, dass sich dann die Zugkraft am Rad linear zur neuen Übersetzung i2 verändert?
Noch was: Ist die Änderung der o.b. Übersetzung mit einer Änderung des Drehmomentes (z.B. über Motortuning) zu vergleichen?
In meinem Fall habe ich original einen Kettensatz von 18/43 Zähnen. Ich habe diesen auf 16/43 verändert, was sich enorm ausgewirkt hat. Natürlich hat sich nicht das Drehmoment des Motors verändert, sondern nur die Zugkraft am Hinterrad.
Hallo Siggi, das stimmt! Du hast mit der 18->16 Übersetzungsänderung die Zugkraft am Rad um 11% gesteigert. Allerdings auch die Höchstgeschwindigkeit in dem Gang um 11% reduziert. :)
Hallo Paul,
vielen Dank für den verständlich formulierten und aufschlussreichen Artikel. Eine Frage hat sich für mich jedoch noch nicht ganz geklärt: Ist am Ende für die Beschleunigungskraft “nur” das Drehmoment relevant (siehe deine Formel zu Fzug), oder spielt hier die “verfügbare Leistung” auch eine Rolle?
Konkretes Beispiel:
Hat der S4 B6 bei 2.500 U/min und bei 5.500 U/min die selbe Beschleunigungskraft (= “Spaß im Kopf durch g-Kräfte”)? Denn das Drehmoment ist in beiden Betriebspunkten gleich, die verfügbare Leistung jedoch mehr als 2x so hoch.
Wenn die Hypothese richtig ist: Wofür wird dann das Mehr an Energie “verbraten”?
(P.S. Alles andere natürlich ceteris paribus, also gleicher Gang, gleiche Räder, …)
Hallo Sebastian,
das siehst du richtig, es ist nur das Drehmoment am Rad entscheidend für die Beschleunigung. Allerdings nur, wenn sich das Rad auch dreht. Und das “drehen” ist ja eigentlich “Umdrehungen pro Zeit” und schon ist man bei der üblichen Berechnung für die Leistung:
P = 2Pi M n
Also Drehmoment multipliziert mit Drehzahl ist die Leistung. Du siehst also, die beiden hängen unmittelbar zusammen. Man kann also nicht beschleunigen ohne Leistung aufzuwenden. Andererseits resultiert aus einer bestimmten Leistung bei einer bestimmten Drehzahl immer ein Drehmoment.
Konkret auf das Beispiel mit den beiden Drehzahlpunkten: Die Beschleunigung wird theoretisch in beiden, also 2500 und 5000 Punkten gleich stark sein. Die zusätzliche “Energie” wird dadurch “verbraten”, dass man einfach schneller ist bei der höheren Drehzahl. Und damit muss sich das Rad schneller drehen und dann kommen wir wieder zu eingangs erwähnten Beschreibungen, nämlich “Leistung ist Arbeit pro Zeit” heraus.
Die Gleichungen zur Berechnung der Zugkraft und der Geschwindigkeit werden schlecht erklärt. Zum einen rätselt der ungeübte Leser, welche physikalischen Größen die Variablen bezeichnen. Bis auf die Übersetzung i wird dieses Wissen vorausgesetzt. Zum anderen werden die Einheiten durch Faktoren umgerechnet, ohne die Einheiten aber anzugeben (v [km/h], n [1/min]).
Dass die Zugkraft F ohne Einheiten (bzw. in Prozent) eingeführt wird, ist irritierend. Den nachfolgenden Hinweis “normiert auf die Fahrzeugmasse” bezieht der Leser auf die Diagramme. Ich weiß nicht, wie das in der Fachliteratur üblich ist. Es scheint mir aber günstiger, zuerst die Formel für Zugkraft anzugeben und diese dann in einem zweiten Schritt mit der Gewichtskraft zu normieren.
Wenn die Kraft auf die Fahrzeugmasse bezogen wird, erhält man die Beschleunigung. Das Verhältnis von Zugkraft zu Gewichtskraft ist also nichts anderes als das Verhältnis von Beschleunigung von Fallbeschleunigung.