Da die Beiträge zum Kalman Filter (Teil1 und Teil2) sowie der Beitrag zum Extended Kalman Filter die am Häufigsten gelesenen des Motorblogs sind, habe ich zum Extended Kalman Filter noch mal einen etwas detaillierteren Screencast aufgezeichnet, welcher recht ausführlich erläutert, wie dieser aufgesetzt wird und arbeitet.
Extended Kalman Filter with CTRV Vehicle Model in Python from Paul Balzer on Vimeo.
Extended Kalman Filter in Python
Das Extended Kalman Filter ermöglicht die Fusion mehrerer verrauschter Sensorsignale unter Zuhilfenahme eines (nicht linearen ) Dynamik-Modells, welches linearisiert wird. Die Linearisierung erfolgt dabei mit so genannten Jacobi Matrizen. Diese können numerisch berechnet werden, wie im Matlab Beispiel zum EKF gezeigt, oder eben analytisch, wie in dieser Python Implementierung. Dank Sympy, dem symbolischen Python Paket, funktioniert das relativ fehlerfrei und komfortabel.
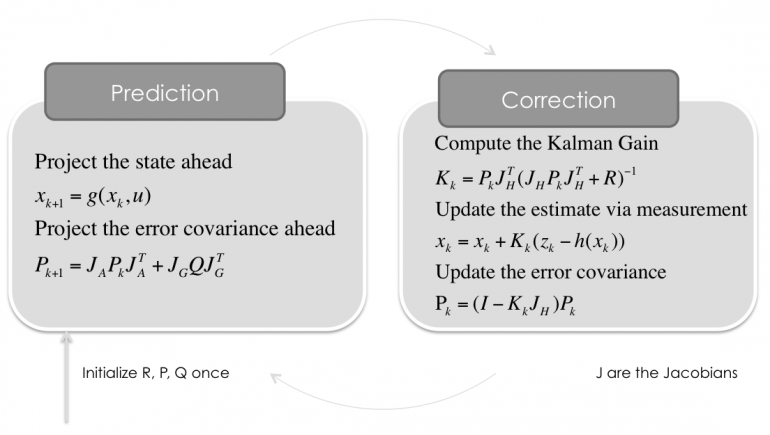
Extended Kalman Filter
Der vollständige Code sowie das IPython Notebook aus dem Video ist auf http://balzer82.github.io/Kalman/ zu finden.
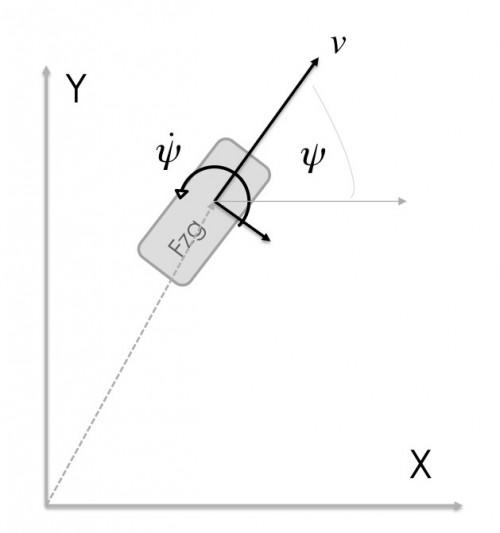
Das implementierte Dynamikmodell ist ein Fahrzeug, welches mit konstanter Geschwindigkeit (zwischen zwei Filterschritten) und Gierrate fährt und nach [Schubert, R., Adam, C., Obst, M., Mattern, N., Leonhardt, V., & Wanielik, G. (2011). Empirical evaluation of vehicular models for ego motion estimation. 2011 IEEE Intelligent Vehicles Symposium (IV), 534–539. doi:10.1109/IVS.2011.5940526] gute Ergebnisse liefert.
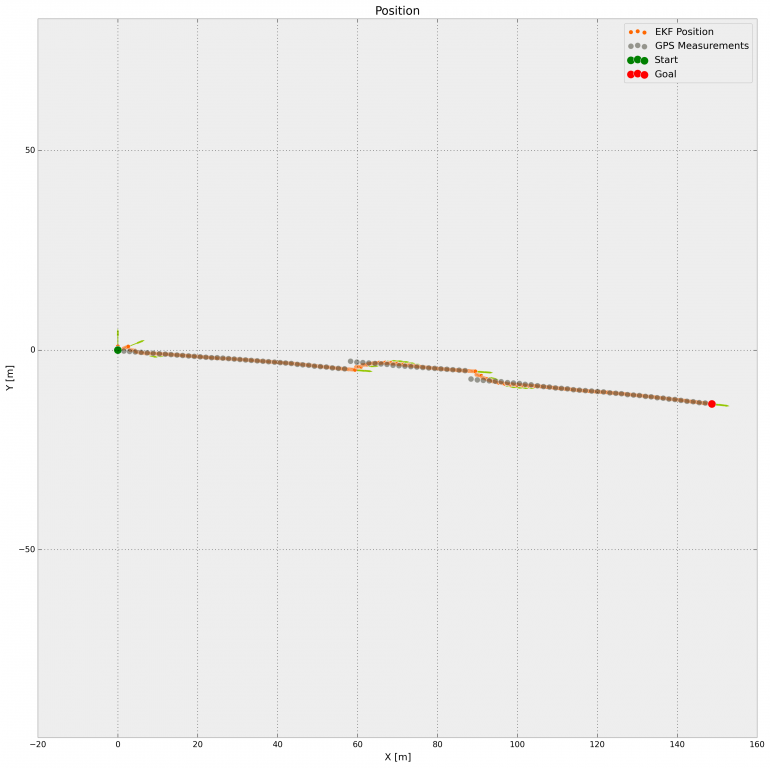
Die Messung der Position erfolgt mit 10Hz und stellt die “Correction” des Systemzustands dar. Der Control Input des Filters ist die Gierrate und Geschwindigkeit, welche genau genommen auch gemessen werden, hier aber als Steuergrößen angenommen sind.
Positionsschätzung des Extended Kalman Filters mit CTRV Modell
3 Comments
Guten Tag Herr Balzer,
erst mal vielen Dank für die schöne Übersicht und Erklärung zum Kalman Filter.
Im Falle der Geradeaus fahrt, also der Gierrate=0, müsste hier nicht eine neue Jacobimatrix von A berechnet werden, da sich das dynamische Modell unterscheidet.
Vielen Dank
Mit freundlichen Grüßen
Björn Beckmann
Hallo Hr Beckmann,
das ist korrekt, genau genommen müsste man das machen. Ich habe diesen “Hack” in die Prädiktion eingebaut, weil es sonst Fälle gibt, in denen das Filter numerisch nicht durchlaufen würde. Es gibt Logfiles, da hat der Drehratensensor keinen Wert geliefert und das Filter müsste durch 0 teilen. Um das abzufangen habe ich die paar Zeilen eingefügt, ohne das konsistent auch auf die Jacobi Matrizen durchzuziehen. Wenn man sich anschaut wie oft er dort in die exakte Geradeausfahrt springt sieht man, dass es sogut wie nie vorkommt. Der Fehler den man durch meine unvollständige Implementierung macht, ist also zu vernachlässigen.
Danke für den Hinweis!
Hallo Herr Balzer!
Die Gleichung zur Prädiktion der Fehlerkovarianz verwirrt mich etwas. Sie weicht von der im Video ab. Warum wird hier die Prozessrauschkovarianzmatrix Q noch von links und rechts mit der Jakobischen von g multipliziert?
lg Michael