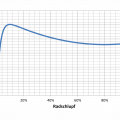
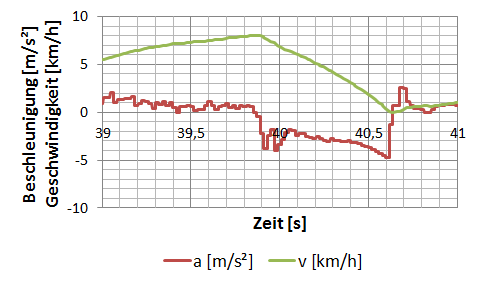
Die Variante, die Daten über ein Videobild zu legen, ist ähnlich, wie mit Kanonen auf Spatzen zu schießen. Das sieht zwar schön aus, aber ist sehr viel Aufwand. Oft reicht es auch aus, die Daten in Diagrammen darzustellen.
Im Folgenden möchte ich zeigen, wie man Daten aus einer Datei in anschauliche Diagramme verpackt und automatisiert abspeichert.
Datenaufzeichnung
Die Daten sind aus der gleichen Quelle, wie im Artikel “Datenvisualisierung mit Matlab”.
Matlab Script zum Erstellen von Diagrammen aus Excel Datei
Das Script ließt Werte aus einer Excel Datei, erstellt verschiedene Diagramme und speichert diese in Druckqualität als .PNG Datei ab. Die Bearbeitung dauert ca. 10s, je nach CPU. Das zeigt, wie überlegen Mathworks Matlab im Vergleich zu Tabellenkalkulationsprogrammen wie Excel ist, wenn es um die Auswertung von Messdaten geht.
1. Excel Datei öffnen und Variablen in Workspace legen
clear all, close all, clc
%% open data file
[filename,path] = uigetfile('*.xls', 'Load XLS File');
if (isequal(filename, 0))
return; % cancel
end
data = xlsread(fullfile(path,filename));
%% Variablen Fahrdynamik
t = data(:,1); %Zeit in s
v = data(:,2); %Geschwindigkeit in km/h
ay = data(:,3); %Querbeschleunigung in g
ax = data(:,4); %Längsbeschleunigung in g
yaw = data(:,5); %Fahrtrichtung in Grad
vv = data(:,6); %Vertical Speed in km/h
nu = data(:,7); %Anzahl Satelitten
B = data(:,8); %Breitengrad in min
L = data(:,9); %Längengrad in min
s = data(:,10);%Weg in m
R = data(:,12);%Kurvenradius in m
dt = diff(t);
dt = dt(1); %Abtastzeit der Daten
%% Filtern um Hochfrequenten Anteil weg zu bekommen
ayf = filter(ones(1,10)/10,1,ay);
yawf = filter(ones(1,10)/10,1,yaw);
%% Rundenzeiten aus Messschrieb
lap0 = 150; %Einführungsrunde
lap1 = lap0 + 136.1;
lap2 = lap1 + 135.8;
lap3 = lap2 + 133.1;
lap4 = lap3 + 134.5;
lap5 = lap4 + 133.9;
% Runde definieren
start = find(t>lap1,1,'first');
stop = find(t>lap2,1,'first');
% Rundenzeiten berechnen für Diagramme
rundenzeit = t(stop)-t(start);
min = fix(rundenzeit/60);
sek = rundenzeit - min*60;
rundenzeit = [num2str(min) ':' num2str(sek)];
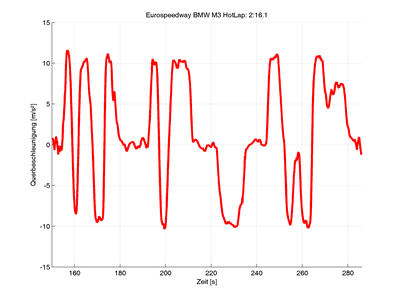
2. Diagramm Querbeschleunigung über Zeit
%% Querbeschleunigung
figure(1)
line(t(start:stop),ayf(start:stop).*9.81,'Color','red','LineWidth',3)
grid on
xlim([t(start) t(stop)])
ylim([-15 15])
title(['Eurospeedway BMW M3 HotLap: ' rundenzeit])
xlabel('Zeit [s]')
ylabel('Querbeschleunigung [m/s²]')
print(gcf,'-dpng','-r300','Querbeschleunigung-Zeit.png')
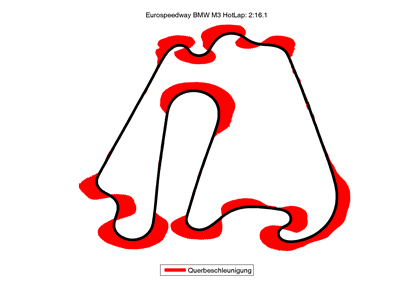
3. Diagramm Querbeschleunigung über Strecke
%% Querbeschleunigung über Strecke
figure(2)
aymaxindex = find(ayf(start:stop)>1.2)+start;
% Beschleunigungssignal einfügen
for i=start:1:stop
ll = -ayf(i)./30; % Skalierung
dL = L(i+5)-L(i);
dB = B(i+5)-B(i);
ld = atan2(dL,dB); % Richtungswinkel bestimmen
ld = ld+pi/2; % Senkrechte dazu
%farbe = abs(ayf(i))/max(ayf); %normieren auf max g
line([B(i) (B(i)+ll*cos(ld))],[L(i) (L(i)+ll*sin(ld))],...
'color',[1 0 0],'LineWidth',5)
end
aymaxindex = find(ayf(start:stop)>1.2)+start;
for i=start:1:stop % nochmal Maxima einfügen
if (i==4289)||(i==4460)||(i==4657)||(i==5170)||(i==5359) %dort sind hohe ay
text('Position',[B(i) L(i)-0.05],'HorizontalAlignment','center',...
'String',{'\uparrow'; [num2str(round(9.81*ayf(i)*100)/100) 'm/s²']})
end
end
%Kurs überlagern
line(B(start:stop),L(start:stop),'LineWidth',4,'color','black')
axis off
title(['Eurospeedway BMW M3 HotLap: ' rundenzeit])
legend('Querbeschleunigung','location','Southoutside')
print(gcf,'-dpng','-r300','Querbeschleunigung-Strecke.png')
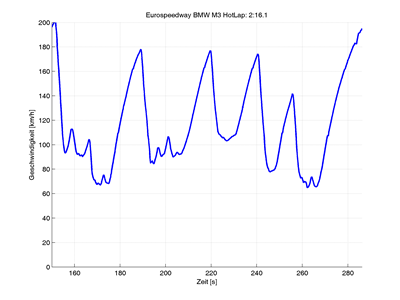
4. Diagramm Geschwindigkeit über Zeit
%% Geschwindigkeit
figure(3)
line(t(start:stop),v(start:stop),'LineWidth',2)
grid on
xlim([t(start) t(stop)])
ylim([0 200])
title(['Eurospeedway BMW M3 HotLap: ' rundenzeit])
xlabel('Zeit [s]')
ylabel('Geschwindigkeit [km/h]')
print(gcf,'-dpng','-r300','Geschwindigkeit-Zeit.png')
5. Diagramm Geschwindigkeit über Strecke
%% Geschwindigkeit über Strecke
figure(4)
% Geschwindigkeitssignal einfügen
for i=start:1:stop
ll = -v(i)./3000; % Skalierung
dL = L(i+5)-L(i);
dB = B(i+5)-B(i);
ld = atan2(dL,dB); % Richtungswinkel bestimmen
ld = ld+pi/2; % Senkrechte dazu
%farbe = abs(ayf(i))/max(ayf); %normieren auf max g
line([B(i) (B(i)+ll*cos(ld))],[L(i) (L(i)+ll*sin(ld))],...
'color',[0 0 1],'LineWidth',5)
end
%Kurs überlagern
line(B(start:stop),L(start:stop),'LineWidth',4,'color','black')
axis off
title(['Eurospeedway BMW M3 HotLap: ' rundenzeit])
legend('Geschwindigkeit','location','Southoutside')
print(gcf,'-dpng','-r300','Geschwindigkeit-Strecke.png')
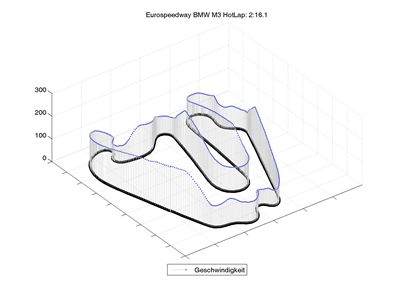
6. Diagramm Geschwindigkeit über Strecke in 3D
%% Geschwindigkeit über Strecke 3D
figure(5);
h=stem3(B(start:2:stop),L(start:2:stop),v(start:2:stop),...
'fill','MarkerSize',2,'MarkerFaceColor',[0 0 1],'Color',[.8 .8 .8]);
hold on
view(143,60)
%Kurs überlagern
line(B(start:10:stop),L(start:10:stop),'LineWidth',4,'color','black')
title(['Eurospeedway BMW M3 HotLap: ' rundenzeit])
legend('Geschwindigkeit','location','Southoutside')
set(gca,'XTicklabel',[],'YTicklabel',[]);
grid on
box off
print(gcf,'-dpng','-r300','Geschwindigkeit-Strecke-3D.png')
close all;
Animation
Wenn man den view Befehl noch etwas variiert, kann man das Diagramm auch noch animieren: