— Dies ist Teil2 der Tutorials zu Neuronalen Netzen – hier ist Teil1: Neuronale Netze einfach erklärt —
 Nach der Einführung in die Thematik der Neuronalen Netze nun ein einfaches Deep Learning Beispiel mit der wichtigsten Bibliothek, welche für das Thema Machine Learning mit Neuronalen Netzen derzeit genutzt wird: Tensorflow!
Nach der Einführung in die Thematik der Neuronalen Netze nun ein einfaches Deep Learning Beispiel mit der wichtigsten Bibliothek, welche für das Thema Machine Learning mit Neuronalen Netzen derzeit genutzt wird: Tensorflow!
Deep Learning ist hauptsächlich (bis auf Forschungsthemen) Supervised Learning, d.h. man zeigt dem Netzwerk also für bestimmte Eingangswerte die richtige Lösung (z.B. Klassifikation von Bildern oder Gruppen), das Netzwerk lernt Schritt für Schritt besser zu werden. Für viele Ingenieurs-Problemstellungen ist die zu schätzende Ausgangsgröße keine einzelne Klasse oder Kategorie (z.B. Auto, Haus, Boot) sondern ein kontinuierlicher Wert, z.B. ein Preis oder eine Kraft oder Fläche o.ä.
Neuronale Netze sind ein universeller Approximator: Wenn es einen Zusammenhang zwischen Ein- und Ausgangsgröße gibt, ist es sehr wahrscheinlich, dass ein (handwerklich korrekt aufgesetztes) Neuronales Netz diesen finden wird. Achtung: Es findet Korrelationen! Ob diese Korrelationen auch einen kausalen Zusammenhang haben oder nicht muss der Experte entscheiden.
Für dieses Tutorial knüpfen wir an Michael Nielsons Tutorial an und versuchen die folgende Funktion \(f(x)\) von einem Netzwerk schätzen zu lassen.
\[f(x)=0.2+0.4x^2+0.3x \cdot \sin(15x)+0.05 \cdot \cos(50x)\]
Ein typisches Regressionsproblem, daher nun ein Tensorflow Tutorial zum DNNRegressor, welches sich prinzipiell auch für höherdimensionale bzw. kompliziertere Fragestellungen nutzen lässt.
Tutorial: Tensorflow DNNRegressor
Die Versionen und damit Tensorflow-APIs ändern sich so schnell, dass viele Google-Treffer zu Tutorials gar nicht mehr aktuell sind und man mitunter an einfachen Dinge hängen bleibt. Dieses Tutorial gilt für die aktuelle Tensorflow 1.4 (kompletter Code am Ende des Beitrags: Bitte scrollen).
Tensorflow ist ein Profi-Werkzeug, allerdings wurden mittlerweile vereinfachte bzw. High-Level API-Enpunkte hinzugefügt, welche es relativ einfach machen zu starten. Wer aus der Welt von SciKit-Learn kommt, wird jetzt hier einen Einstieg finden. Das Skflow Projekt wurde mittlerweile als contrib/learn in Tensorflow integriert, ist also gekommen, um zu bleiben (hoffentlich). Dazu importieren wir ein paar Dinge:
import tensorflow as tf import tensorflow.contrib.learn as skflow from sklearn.model_selection import train_test_split import numpy as np
Nun können wir los legen.
Problem Statement: Wir haben Daten (Features) und ein Zielwert (Labels)
Da wir ein einfaches, nachvollziehbares Tutorial durchgehen, sind unsere Eingangsdaten einfach nur eine Reihe von Zahlen, denn mehr brauchen wir erst mal nicht. Wir erzeugen uns als Eingangsdaten 1mio Zahlen, aufsteigend zwischen 0 und 1 und als Spaltenvektor umgeformt:
X = np.linspace(0, 1, 1000001).reshape((-1, 1))
Was das Netzwerk lernen soll müssen wir auch künstlich erzeugen, wir nehmen die oben genannte Funktion:
f = lambda x: 0.2+0.4*x**2+0.3*x*np.sin(15*x)+0.05*np.cos(50*x) y = f(X)
Nun haben wir unsere Features in \(X\) und unsere Labels in \(y\). Wobei die Bezeichnung für ein Regressionsproblem nicht ganz korrekt ist, aber im Allgemeinen wird dies für Machine Learning Probleme so bezeichnet.
Trainings- und Testdaten vorhalten
Um eine Aussage zur Qualität der Prädiktion treffen zu können, sollten wir von unseren Daten etwas abzweigen, was wir dem Netzwerk während des Lernprozesses nicht zeigen. Das ist der so genannte Train/Test-Split, welchen wir ganz komfortabel in SciKit-Learn implementiert haben.
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.1, random_state=2)
Wir nutzen 10% der Daten zum testen der Vorhersage und trainieren mit 90% der Daten.
Training und Test des DNNRegressor mit Tensorflow numpy_input_fn
Eine Möglichkeit Tensorflow mit Daten zu versorgen ist die numpy_input_fn. Wir generieren eine für das Training und später noch eine zum Evaluieren (Testen).
def training_input_fn(batch_size=1):
return tf.estimator.inputs.numpy_input_fn(
x={'X': X_train.astype(np.float32)},
y=y_train.astype(np.float32),
batch_size=batch_size,
num_epochs=None,
shuffle=True)
Was wurde hier gemacht? Die Funktion training_input_fn() gibt einfach nur die Tensorflow numpy_input_fn() zurück. Diese benötigt für die Eingangsdaten x ein Dictionary, welches wir mit dem Namen “X” versehen und mit den Werten aus X_train füllen. Die Typzuweisung (float32) ist hier nicht unbedingt nötig, jedoch möchte ich explizit darauf hinweisen, dass dies gut wäre, denn GPUs verlangen float32 und alle Input Funktionen müssen den gleichen Datentyp haben. Zum Trainieren wird die Anzahl der Epochen auf None gesetzt.
Design eines Neural Networks mit Tensorflow
Nun designen wir das Neural Net für Tensorflow. Wir nutzen den DNNRegressor aus tf.contrib.learn. Schaut man auf die Instantiierung, so gibt es viele (optionale) Parameter, welche wir nicht alle benötigen.
regressor = skflow.DNNRegressor(feature_columns=feature_columns, label_dimension=1, hidden_units=hidden_layers, model_dir=MODEL_PATH, dropout=dropout, config=test_config)
Einige Variablen möchte ich im folgenden erläutern:
Zum Instantiieren ist eine feature_column notwendig, welche Tensorflow sagt, was für Daten eingespeist werden. Für das Regressionsproblem ist eine numerische Spalte der Breite 1 die korrekte Eingangsdefinition, denn die Funktion f(x) ist nur von einem eindimensionalen x abhängig. Für andere Problemstellungen sind auch noch andere und auch kombinierte Spalten möglich, siehe.
feature_columns = [tf.feature_column.numeric_column('X', shape=(1,))]
Da unser Regressionsproblem 1-dimensional ist (eine Funktion f(x) gibt ein eindimensionales y zurück), wird die label_dimension auf 1 gesetzt. Für mehrdimensionale Problemstellungen, z.B. Lat/Lon Positionsschätzungen in der Ebene, muss dies entsprechend auf 2 gesetzt werden.
Weiterhin definieren wir ein paar Variablen, welche das Design des Netzwerks beschreiben:
hidden_layers = [128, 64, 32] dropout = 0.0
Was haben wir hier definiert?
- hidden_layers ist die Anzahl der Neuronen pro Layer, in diesem Beispiel ein Netzwerk mit 3 Hidden Layers,
- 1. Layer 128 Neuronen
- 2. Layer 64 Neuronen
- 3. Layer 32 Neuronen
- dropout ist der Anteil an Neuronen der während jeden Lernschritts pro Layer zufällig ignoriert wird, d.h. nicht am Lernprozess (fitting) teilnimmt
- Dies ist für viele praktische Anwendungsfälle empfohlen, um das Netzwerk daran zu hindern einfach nur alles auswendig zu lernen an statt generalisiert wiederzugeben, siehe.
- Allerdings dauert das lernen dann wesentlich länger und die Ergebnisse sind nicht immer zufriedenstellend
- Warum das funktioniert ist noch Gegenstand der Forschung, wir Menschen lernen z.B. auch, indem wir einige Dinge einfach wieder vergessen. :)
- MODEL_PATH ist der Pfad auf der Festplatte, wo Tensorflow alles speichern soll
- kann für Tensorboard genutzt werden
- wird zum laden des Modells (wenn es trainiert ist) genutzt
- wird zum ‘später weiter trainieren’ genutzt
- test_config kann genutzt werden um das Speichern in der MODEL_DIR zu parametrieren, siehe
Fertig. Zeit zum lernen.
Training eines Neuronalen Netzwerks mit Tensorflow DNNRegressor
Dies ist nun der einfachste Teil. Wir lassen für mehrere Epochen das Netzwerk den Fehler ermitteln und auf die Neuronen verteilen. Dies passiert bei geeigneter Hardware automatisch auf der GPU (NVIDIA CUDA vorausgesetzt), sonst auf der CPU. Für dieses kleine Problem auch nicht relevant, denn das kopieren von/zu Grafikkarte kostet auch Zeit und da ist man mitunter auf einer CPU schneller.
for epoch in range(EPOCHS): # Fit the DNNRegressor (This is where the magic happens!!!) regressor.fit(input_fn=training_input_fn(batch_size=BATCH_SIZE), steps=STEPS_PER_EPOCH)
Was haben wir hier noch zusätzlich als Variablen definiert?
- BATCH_SIZE ist die Anzahl an Daten die gleichzeitig zum lernen genutzt werden sollen.
- Für uns irrelevant, wir könnten praktisch immer mit den gesamten Daten trainieren
- Aber für größere Problemstellungen (z.B. für Bildverarbeitung), wo die Tensoren (=Eingangsdaten) groß sind [batch_size, height, width, channels], steuert die BATCH_SIZE wieviel Daten (z.B. Bilder) gleichzeitig auf die GPU kopiert werden zum training
- begrenzt z.B. durch den RAM der GPU
- STEPS_PER_EPOCH: Wieviel mal Tensorflow pro Ausführen des .fit() die Fehler backpropagieren (auf die Neuronen verteilen) soll
- EPOCHS: Wie oft wir .fit() ausführen wollen
Das sieht jetzt erst mal komisch aus, denn man könnte ja auch einfach nur 1 Epoche laufen lassen, dafür aber steps größer wählen. Das stimmt, doch es gibt auch Fälle, wo die input_fn() beispielsweise Daten aus verschiedenen Dateien erst mal lädt oder Datenbankabfragen macht oder die Daten jeweils generieren muss oder der RAM einfach zu klein ist für alle Daten gleichzeitig und dann kann man es auf Epochen verteilen. Andere Möglichkeiten Daten zu lesen.
Tensorflow bekommt jetzt die Daten aus X_train als Eingang, versucht y_train korrekt zu schätzen, macht dabei Fehler (für Regressionsprobleme typisches Fehlermaß ist der mittlere Abstand von geschätzter Funktion zu realer Funktion: MSE), der DNNRegressor (de-)aktiviert die Neuronen die ihn verursacht haben und wird Step-by-Step besser:
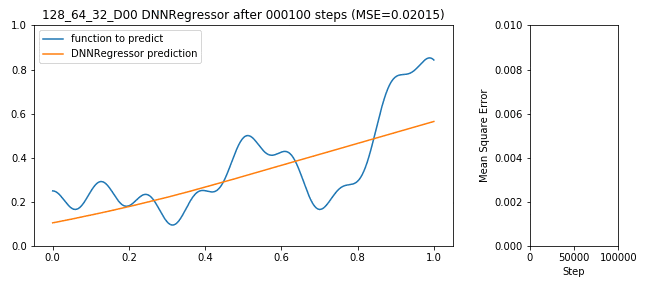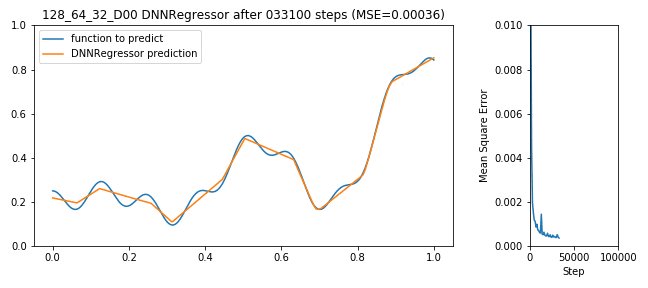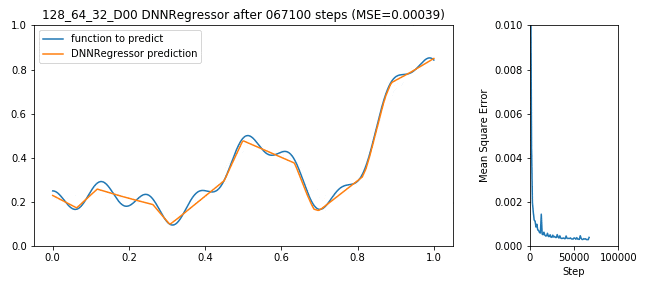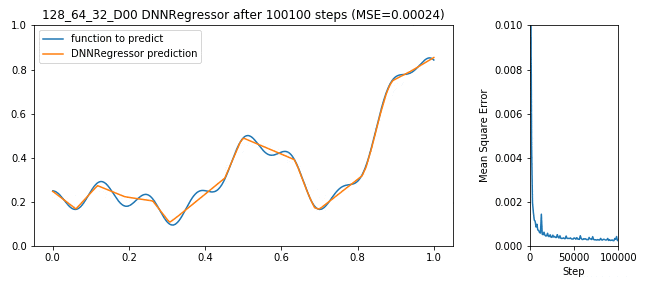
128x64x32 DNNRegressor learning to predict a function
Soweit so gut, der Fehler geht nach unten, das Netzwerk lernt, alles richtig gemacht. Das war einfach. Doch die Frage bleibt: Ist das schon das beste Ergebnis? Länger lernen? Mehr Neuronen im 1. Layer oder mehr im 2. oder vielleicht Dropout? Und wer sagt, dass 3 Layer gut sind? Vielleicht 10 oder vielleicht nur ein Layer mit 100000 Neuronen?
Das ist die Kunst! Hier braucht es Werkzeuge, Erfahrung, Zeit, Rechenzentren und Tensorboard.
Evaluation von Neuronalen Netzen mit Tensorboard
Der von uns genutzte DNNRegressor hat eine Methode namens .evaluate() und diese können wir nutzen um ihn zu… na, wer errät es?
eval_dict = regressor.evaluate(input_fn=test_input_fn(), metrics=validation_metrics)
Wir nutzen eine andere Input Function zum testen, welche X_test und y_test (vom Train/Test Split) an Tensorflow liefert:
def test_input_fn():
return tf.estimator.inputs.numpy_input_fn(
x={'X': X_test.astype(np.float32)},
y=y_test.astype(np.float32),
num_epochs=1,
shuffle=False)
Hier wird Shuffle auf False gesetzt und die Anzahl der Epochen auf 1: Einfach nur 1x genau so wie definiert mit X_test und y_test durchrechnen lassen.
Die Validation Metric (also was wir evaluiert haben wollen) können wir aus tf.contrib.metrics bemühen.
validation_metrics = {"MSE": tf.contrib.metrics.streaming_mean_squared_error}
Sobald der Regressor mit fit() trainiert und/oder evaluiert wird, werden im MODEL_PATH Daten geschrieben, die wir mit Tensorboard ganz komfortabel einsehen können. Dazu einfach in einem Terminal Tensorboard starten (logdir sollte MODEL_PATH sein, unter Windows den Pfad vollständig angeben):
tensorboard --logdir='./DNNRegressors/'
Im Browser kann man nun unter localhost auf Port 6006 folgendes sehen:
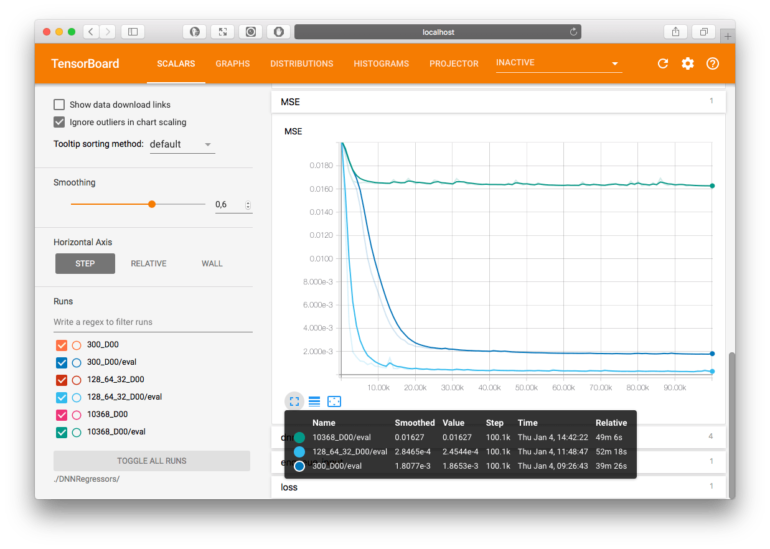
Tensorboard mit Darstellung von Mean Square Error (MSE) von 3 Neuronalen Netzwerken
Tensorboard ermöglicht es u.a. den Lernerfolg zu visualisieren und zu vergleichen. In oberer Darstellung sind beispielsweise 3 verschiedene Netzwerke zu sehen, welche mit der test_input_fn() evaluiert werden.
Vergleich von Neural Network Designs
Neuronale Netze sind ein universeller Approximator, d.h. prinzipiell ist es möglich schon mit nur einem Hidden-Layer eine 1-D Funktion zu approximieren. Ob dies praktisch auf einem Computer dann auch gelingt, ist auch vom Zufall abhängig, denn je nachdem wie Variablen initialisiert werden, dauert das Verteilen der Fehler (Backprop) entsprechend lange, bis es besser wird bzw. bis man aus einem lokalen Minimum wieder heraus optimiert. Im Beispiel hier breche ich jeweils nach 100.000 Schritten ab.
3-Hidden-Layer – 128x64x32 Netzwerk
Schaut man sich die hellblaue MSE Kurve in der Tensorboard Abbildung an, sieht man einen wunderbaren Loss-Function Verlauf, so soll es sein. Die Frage ist: Geht es besser?
“Besser” kann jetzt heißen den MSE zu reduzieren, es kann aber auch heißen weniger RAM zu verwenden, schneller den Vorwärtspfad berechnen zu können (.predict() ist ja das, was man in der Realität von so einem Netzwerk dann möchte), schneller trainieren zu können, oder oder oder, sodass sich die Frage stellt, ob es nicht auch mit einem Layer gehen würde?!
1-Layer – 300 Neuronen Netzwerk
Weniger Neuronen und Layer bedeutet auch weniger zu berechnen, d.h. der Trainingsvorgang geht schneller. In unserem Beispiel lächerlich aber für reale Fragestellungen ist es schon relevant, ob das Netzwerk überhaupt in der Lebenszeit des Engineers ein Ergebnis ausspuckt oder während der Mittagspause schon erste Evaluationen bestimmen kann. Schaut man in Tensorboard die Wall-Time an, so sieht man, dass das 1-Layer Netzwerk mit 300 Neuronen im Vergleich rund 25% schneller trainiert war (39min statt 52min).
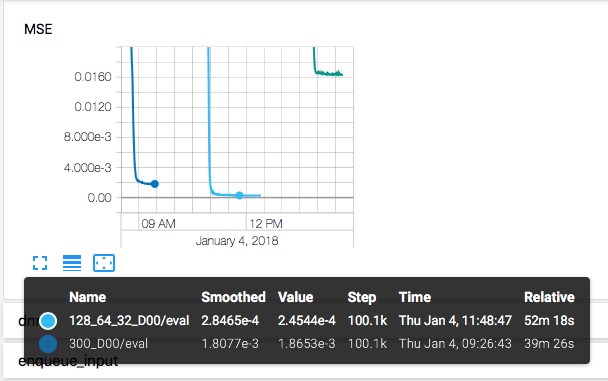
Allerdings kann es auch schlechter die Funktion approximieren. Je nach Anwendungsfall kann dies ausreichend sein, wenn dafür weniger Rechenzeit oder auch Arbeitsspeicher benötigt wird (mobile Anwendungen auf dem Smartphone oder RaspberryPi o.ä.).
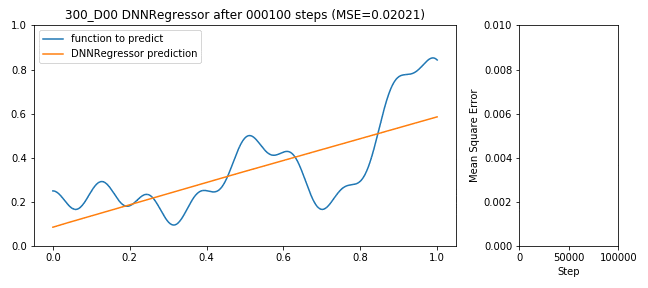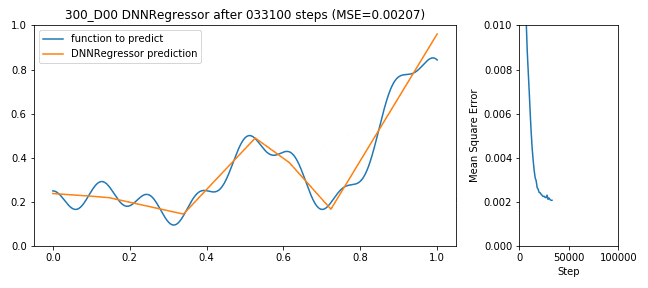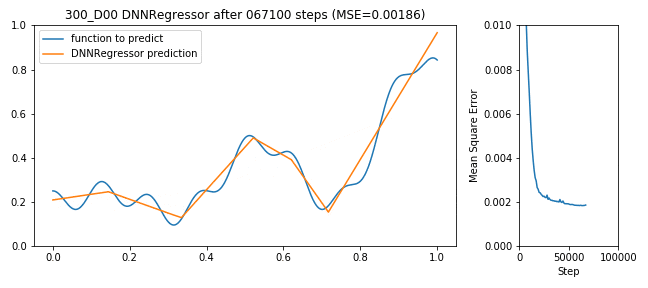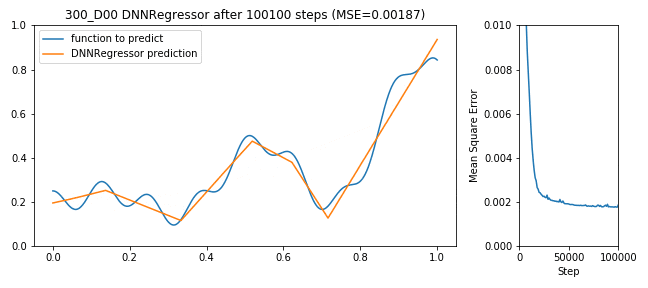
300 neuron shallow DNNRegressor learning to predict a function
Nun kann man argumentieren, dass ein 128x64x32 DNN wesentlich mehr Neuronen und damit Gewichte zum ‘lernen’ hat (nämlich 1×128 + 128×64 + 64×32 = 128 + 8192 + 2048 = 10368) als nur 300. Wie sieht es also aus mit einem Shallow-Network (also flach statt tief)?
1-Layer – 10368 Neuronen Netzwerk
Das ist sehr flach und gar nicht Deep, hat aber genauso viele Gewichte zum aktivieren wie das soeben besprochene 128x64x32 Deep Neural Network. Wie man an der Tensorboard Abbildung (siehe oben) in grün sieht, ist das Netzwerk nicht aus einem lokalen Minimum heraus gekommen und ist damit konkurrenzlos schlecht (es kann sein, dass es bei nochmaliger Wiederholung anders läuft oder auch zu einer späteren Zeit das lokale Minimum überwindet und dann doch noch besser wird, man weiß es nicht)
Tipps zum Design und Training eines Neuronalen Netzwerks
Grundsätzlich gibt es nicht die goldene Regel, wie es immer am besten funktioniert, aber ein paar Rules of Thumb kann man geben:
- lieber tief statt flach, siehe Pascaneu et.al.: “On the number of response regions of deep feedforward networks with piecewise linear activations”, d.h. mehr Hidden Layer statt vieler Neuronen
- aber nicht zu tief, siehe The Vanishing Gradient Problem, d.h. nicht unnütz viele Layer
- so wenig Neuronen wie möglich, so viele wie nötig
- wenn du denkst es hat lang genug gelernt weil nichts mehr passiert, lass es noch mindestens 3x so lange trainieren
- die Loss-Function sollte zu Beginn nicht zu stark fallen, siehe “Babysitting the training process”
- man hat relativ schnell gute Ergebnisse aber die letzten 10% heraus zu holen dauert lang, sehr lang
- die letzten 1% erreicht das Netzwerk vielleicht nie
Alles Tipps beachtet hier nun der Vergleich der oben Evaluierten drei Netzwerke mit einem 5-Layer Deep Neural Network mit je nur 16 (!) Neuronen:
5-Layer – 16x16x16x16x16 Neuronen Netzwerk
Nach 350.000 Trainingsschritten kann dieses kleine Netzwerk die Funktion schon relativ gut approximieren, für die meisten Anwendungsfälle ist ein Modell gefunden worden, welches die Realität (die Funktion f(x)) hinreichend gut abbildet:
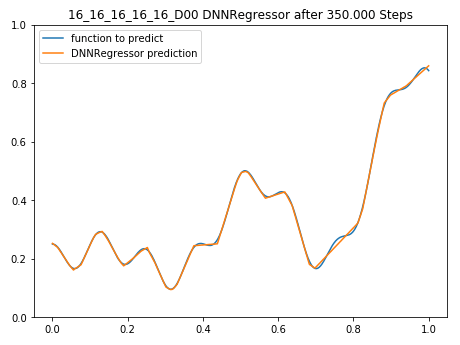
5-Layer Deep Neural Network after 350.000 training steps predicting a function
Im Vergleich zu den anderen besprochenen Netzwerken die MSE Evaluation Kurve, bei der deutlich wird, dass “noch etwas länger trainieren lassen” durchaus eine gute Idee ist.
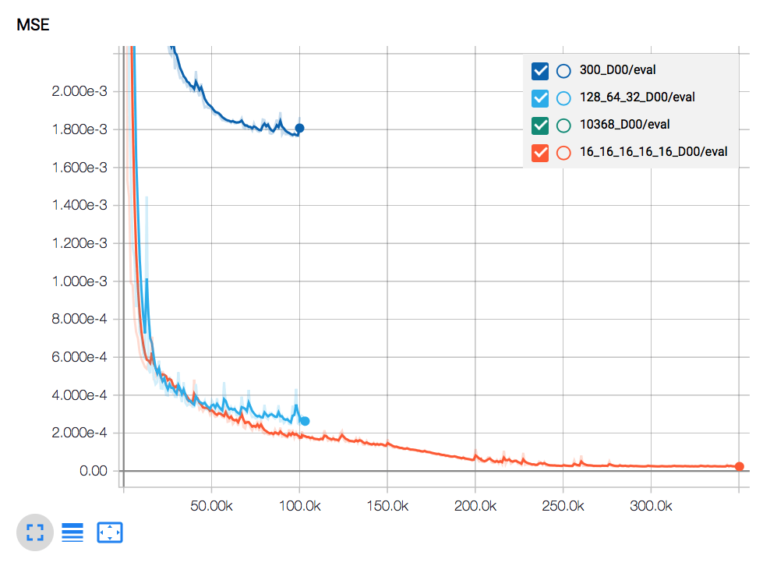
Tensorboard Darstellung der MSE Evaluation
Im Code liegt die Wahrheit, hier nun der gesamte Code zum selbst probieren:
Tensorflow DNNRegressor in Python
Ach übrigens: Für kommerzielle Anfragen gibt es auch die Möglichkeit mich zum Thema zu konsultieren: Hire me!
Was nicht gelernt wurde: Allgemeines Verständnis worum es geht
Wer nun glaubt, dass das Neuronale Netz etwas von Sinus und Cosinus verstanden hat und nebenbei noch die Fourierreihe für f(x) mit gefunden, der täuscht sich! Mit einem einfachen Beispiel kann gezeigt werden, dass das Netzwerk nur das kann, was ihm gezeigt wurde und kein Fähigkeiten aufgebaut hat, die gegebene Funktion ‘zu verstehen’: Erweitert man den Wertebereich für x und lässt das Netzwerk die Funktion f(x) für x={1…1,2} schätzen, so zeigt sich eine riesige Diskrepanz:
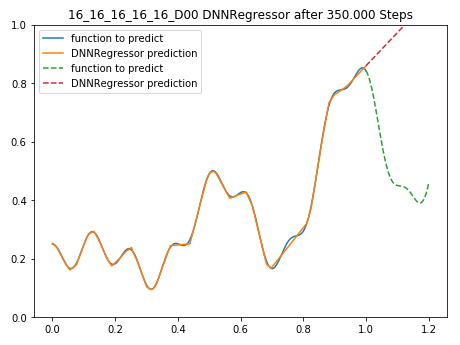
Das 5-Layer 16x16x16x16x16 Netzwerk versucht die Funktion außerhalb des gelernten Wertebereichs zu schätzen, grün=tatsächliche f(x), rot=DNNRegressor prediction
Diese Einschränkung von Neuronalen Netzen muss man immer im Hinterkopf behalten. Man sollte sie keine Dinge fragen, welche außerhalb ihres “Horizonts” liegen.
Es gibt Neuronale Netzwerke, welche Menschen in Objekterkennung o.ä. outperformen, d.h. bessere Erkennungsraten haben als Menschen. Man könnte meinen diese Netzwerke sind nun ‘besser’ als der Mensch. Eine einfaches invertieren der (Eingangsdaten) Bilder (d.h. aus weiß wird schwarz) reicht aus, um diese Netzwerke völlig zu verwirren (siehe “On the Limitation of Convolutional Neural Networks in Recognizing Negative Images“). Uns als Menschen wäre es egal ob eine weiße 1 auf einem schwarzen oder eine schwarze 1 auf einem weißen Hintergrund zu sehen ist. Einem Neuronalen Netz nicht, es muss beide Varianten ‘sehen’ während des trainings, um korrekt zu klassifizieren! Unglaublich dumm aber doch so logisch.
Ein allgemeines Verständnis von dem was das Netzwerk während des trainings “lernt” kommt ohnehin nicht auf. Ein Netzwerk kann alle Flugzeuge der Welt korrekt auf einem Bild klassifizieren, was es heißt zu fliegen, davon hat es keine Ahnung. Diese ‘General AI’ wird es wohl auf absehbare Zeit nicht geben. Mehr dazu in dem tollen Interview mit Zukunftsforscher Alexander Mankowsky von Daimler AG:






3 Comments
Ich habe Ihr Modell mit einem Datensatz mit 7 Input Features und 1 Output Label nachgebaut.
Das Training funktioniert auch problemlos.
Das predicten nach dem Training funktioniert aber nicht.
So habe ich Testweise
X_pred = np.linspace(0,1,11)
durch X_pred =[ [1,1 ,1 ,1 ,1 ,1,1]]
ersetzt, aber komme auf keine Lösung.
Hätten Sie hierfür einen Tipp für mich?
Hallo! Vielen Dank für die Übersicht und den kommentierten Code. Hat mir sehr gut zum Einstieg geholfen. Profitiere ich nun schon länger davon. Alles Gute!