FFT mit Excel

by Paul Balzer on 12. August 2013

21 Comments

Kaum zu glauben aber wahr: Die Artikel über FFT mit Matlab sowie fast alle Excel Beiträge sind immer in den Top10 dieses Blogs. Die zahlreichen EMails und Kommentare dazu, welche hauptsächlich verzweifelte fragende Studierende absetzen, zeigen mir, dass es zu diesen Themen großes Interesse gibt.

Da in vielen Firmen Diplomanden, Praktikanten oder auch Ingenieure ohne adäquate Software ausgestattet sind, aber trotzdem ein Amplitudenspektrum eines Signals berechnen wollen, kann man sich auch mit Microsoft Excel behilflich sein. Hierfür ist das Add-In “Analyse-Funktion” (FUNCRES.XLAM) notwendig.

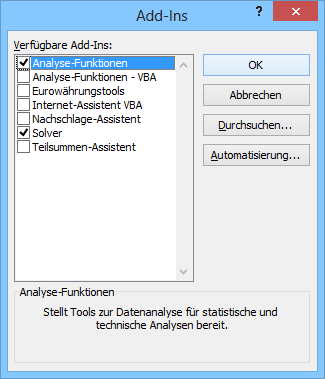Add-InsDieses kann über die Office-Button > Excel Optionen > Add-Ins > Gehe Zu… installiert werden.

Danach steht im Reiter “Daten” in Excel die Funktion “Datenanalyse” zur Verfügung, welche auch die Fourieranalyse beinhaltet.

Fourieranalyse

Die Fourieranalyse ist ein mathematisches Konstrukt, welches erlaubt eine periodische Funktion mit Hilfe von sinus und cosinus Funktionen zu beschreiben.

Ein Computer kann aber ohnehin keine kontinuierlichen Funktionen speichern, weshalb die Fourieranalyse nur ein theoretisches Verfahren der analytischen Mathematik bleibt.

Diskrete Fourier Transformation

Jetzt wird die Sache schon interessanter, denn die Diskrete Fourier Transformation (DFT) erlaubt es für diskrete Signale anteilige Frequenzen zu bestimmen. Jedes Signal, welches mit einem Computer abgespeichert oder aufgezeichnet wird, ist diskret. Leider hat die DFT einen Nachteil: Sie dauert ewig!

f_m = \sum_{k=0}^{2n-1} x_k \;e^{-\frac{2\pi i}{2n} mk }

Kluge Köpfe sind in der Vergangenheit auf die Idee gekommen, dass man die aufwendigen Multiplikationen so aufteilen kann, dass aus einer DFT eines Signals der Länge k auch zwei DFT’s der Länge k/2 gemacht werden können. Diese werden dann in gerade und ungerade aufgeteilt und immer weiter auseinander genommen.

Ohne jetzt weiter in’s Detail zu gehen, aber es kommt eine schnellere Berechnungsabfolge heraus, welche auch Fast Fourier Transformation (eigentlich Fast Diskrete Fourier Transform) genannt wird.

Die Berechnungsdauer der DFT für ein 1min Musikstück, welches mit 44kHz abgetastet gespeichert wurde, dauert auf einem Rechner, der für einen Berechnungsschritt 0.2µs:

t_\text{DFT}=0{,}2 \mu s \cdot (2^{21})^2 \approx 10 \text{Tage}

Fast Fourier Transformation

Der Geschwindigkeitsunterschied zur DFT ist beachtlich! Eine FFT eines 1min Musikstücks, welches mit 44kHz abgetastet wurde dauert mit dem FFT Algorithmus:

t_\text{FFT}=0{,}2 \mu s \cdot \cfrac{2^{21}}{2} \cdot \cfrac{\log(2^{21})}{\log(2)} \approx 4{,}4s

Aus 10 Tagen wurden 4,4 Sekunden auf dem gleichen Rechner! Das ist eine Ansage. Der FFT Algorithmus ist so schnell, dass er sogar in Echtzeit Anwendung findet, etwa bei digitalen Filtern, welche im Smartphone eine Rauschunterdrückung oder Echokompensation vornehmen. Auch das Aufzeichnen eines .mp3 benötigt eine FFT.

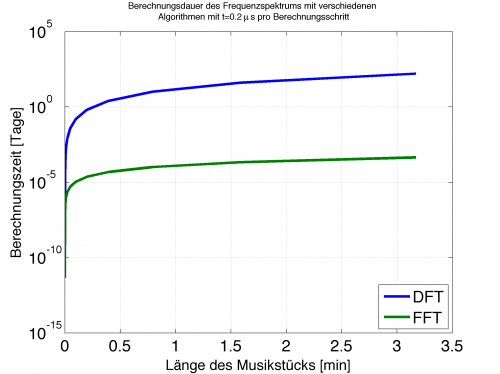
Vergleich der Berechnungsdauer zwischen FFT und DFT für ein Musikstück. Zu beachten die logarithmische Skalierung der Y-Achse! 100 = 1 Tag, 101=10 Tage.

Vergleich der Berechnungsdauer zwischen FFT und DFT für ein Musikstück. Zu beachten die logarithmische Skalierung der Y-Achse! 10-5 = 0,864s, 100 = 1 Tag, 101=10 Tage.

FFT mit Excel

Eine FFT mit Matlab zu machen ist kein Kunstwerk, dafür gibt es den fft() Befehl. Aber in Excel nicht. Mit dem folgenden 5-teiligen Videotutorial möchte ich es trotzdem erläutern.

Einführung und Grundlagen

Weshalb der Algorithmus nur 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 oder 4096 Werte verarbeiten kann.

Wie gesagt, die FFT ist für periodische Funktionen gedacht. Hat man eine Periode, welche nicht mit 4096 Werten beschrieben werden kann, ist mit der Excel FFT keine Information zu bekommen. Eventuell könnte man die Abtastrate reduzieren oder downsamplen (nur jeden x-ten Wert nehmen) oder nochmal drüber nachdenken, ob das Sinn macht, was man gerade vor hat.

Hat man zu wenig Werte um auf z.B. 64 zu kommen, so kann man einfach 0 anhängen, bis die Zahlen erreicht sind.

Signal erzeugen

Shannon Theorem, Antialiasing und weshalb eine Audio-CD mit 44.1kHz gesampled ist.

Add-In und komplexes Amplitudenspektrum (FFT)

Wie man das Add-In “Analyse-Funktion” (FUNCRES.XLAM) installiert und die Durchführung der FFT.

Signal, Rauschen & Gleichanteil

In diesem Teil wird geklärt, wie man den Bezug zur Frequenz herstellt oder anders ausgedrückt: Was an die x-Achse (Frequenzachse) kommt.

Die x-Achse des Amplitudenspektrums berechnet sich wie folgt:

X_i=\cfrac{f_a}{n}\cdot t_i \cdot f_a

Wobei mit x der Wert der X-Achse an der Stelle i gemeint ist. fa ist die Abtastrate, n die Anzahl der Wert (64, 128, 256…) und t die Zeit.

Amplitude der FFT korrekt darstellen

Abschließend wird erläutert, wie man die y-Achse, also die Amplitude nach der FFT wieder korrekt dimensioniert.

Y_i=\cfrac{2 \cdot y_i}{n}

Fazit

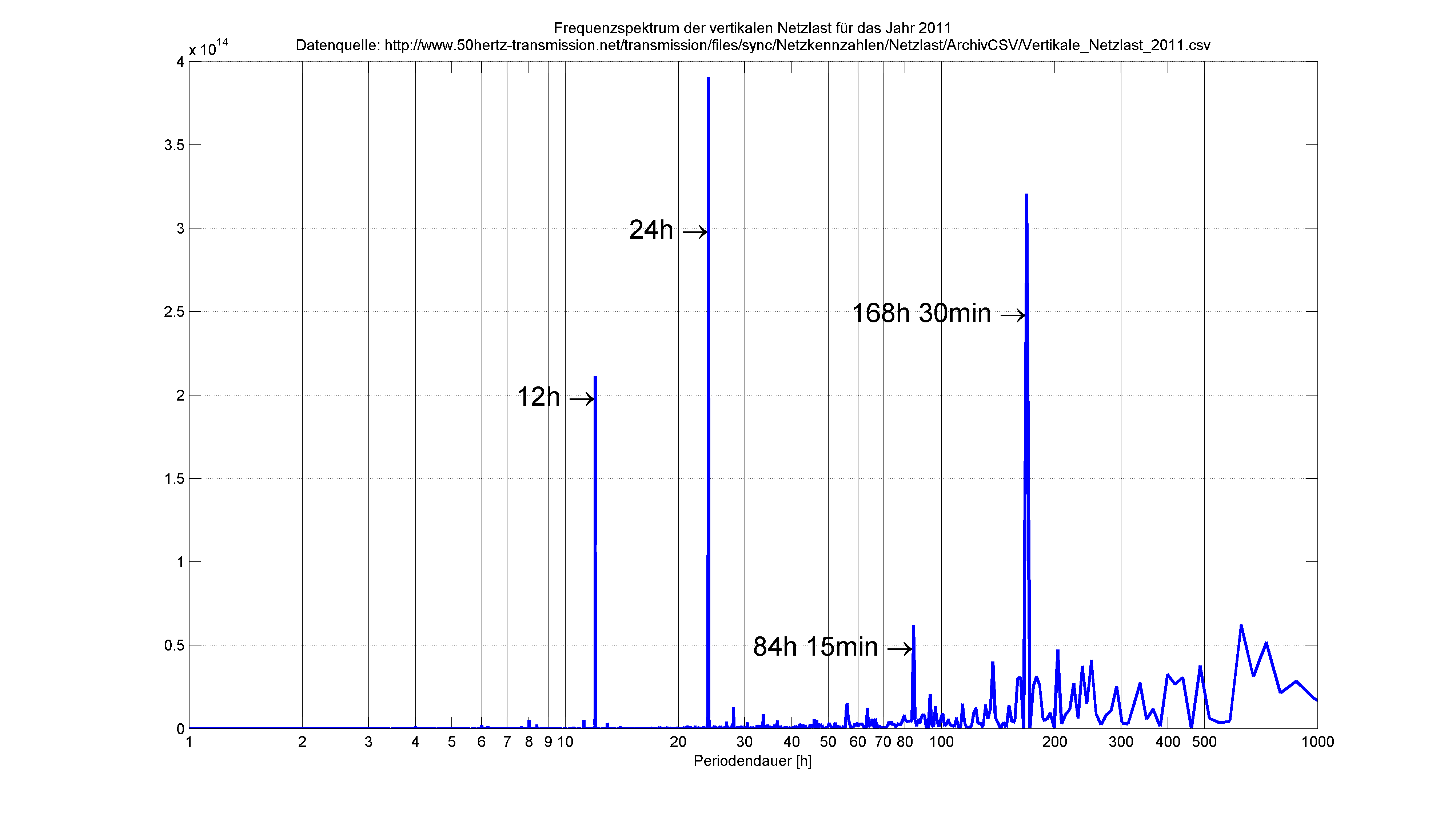
Es ist etwas unhandlicher mit Excel eine FFT zu berechnen, unhandlicher jedenfalls als z.B. mit Matlab, aber es funktioniert und man kann sich zur Not behelfen und eine Messreihe auch auf im Frequenzbereich anschauen. Hat man diese Dimension noch zur Beurteilung von Vorgängen, so erschließen sich bestimmte Zusammenhänge wesentlich besser als bei der reinen Beurteilung von Zeitverläufen.

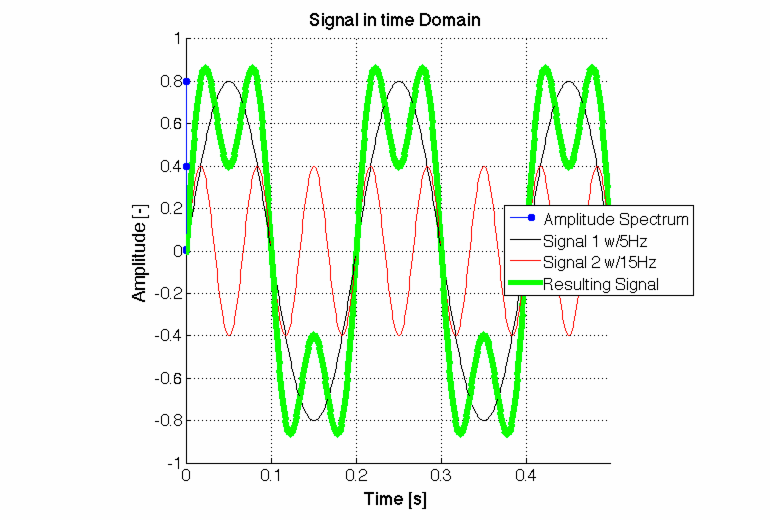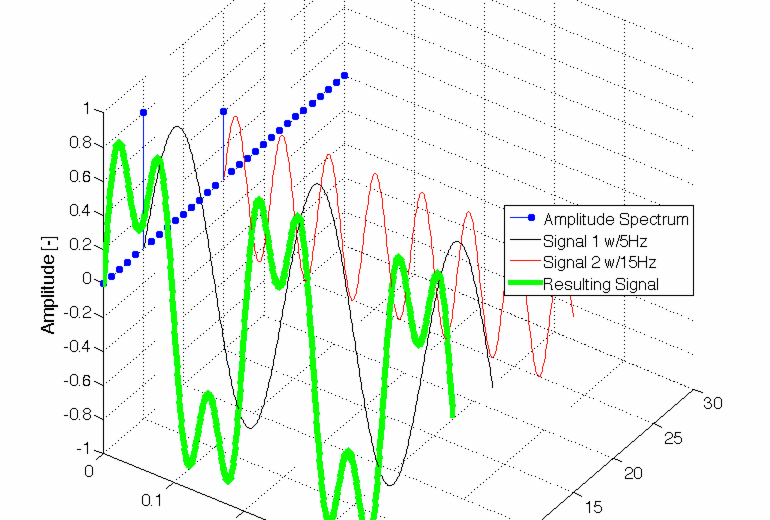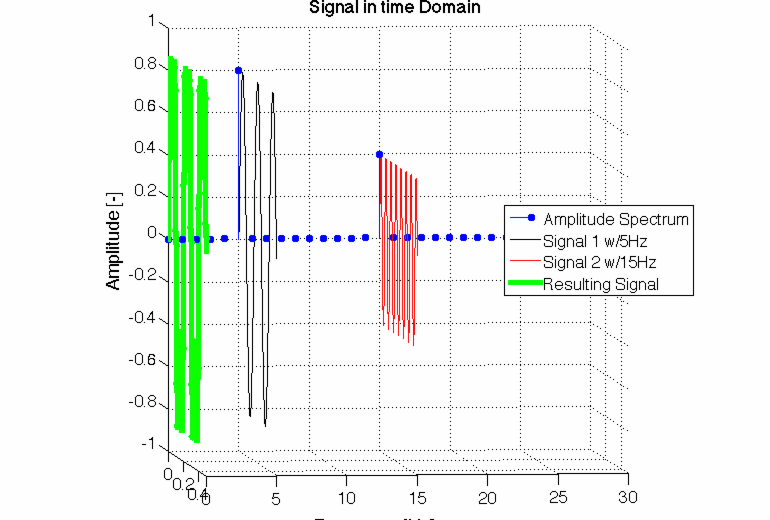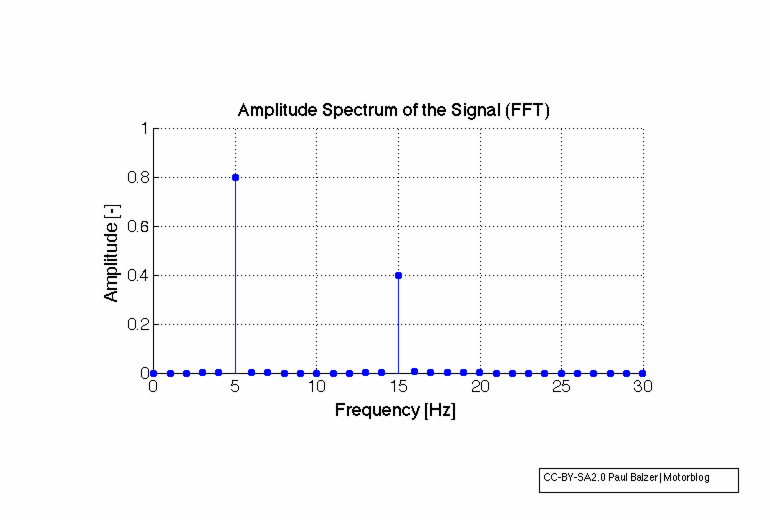
CC-BY-SA2.0

CC-BY-SA2.0

  Download FFT Excel Sheet

Das interessiert dich vielleicht auch:

Frequenzspektrumanalyse (FFT oder DFT) mit Matlab Numerische Integration mit Excel Schwingungsdifferentialgleichung numerisch lösen mit Excel

21 Comments

  1. Hi,
    zum Thema FFT würde ich noch das Stichwort “Fensterung” einwerfen wollen. Das hilft nämlich komische Effekte der FFT zu eliminieren, die durch das Betrachten eines begrenzten Zeithorizonts auftreten.

    Antworten
  4. Pingback: Motorblog » This Animation will tell you everything about the connection between time and frequency domain of a signal

  5. Ich benötige die FFT im Rahmen einer Facharbeit und Deine Anleitung ist höchst anschaulich, so dass ich mir einiges an Recherchearbeit sparen kann: Vielen Dank dafür!

    Antworten

  6. Lieber Herr Balzer,

    Wie kann ich FFT automatisieren bzw. wie eine Excel-Funktion brauchen? Es geht mir darum, ein Signal mit sagen wir 100’000 Samples (eingelesen in 1 Spalte in Excel, wie in Ihrem Beispiel, nur viel länger) mit einer 256-Punkte FFT überlappend abzuarbeiten und ein Spektralprofil (Power in Band) auszurechnen. Das ganze soll in einem Worksheet Platz finden und neu rechnen, sobald ich eine neuen Datenvektor mit 100’000 Samples einfüge. Es ist äusserst unpraktisch, entlang der Spalte x-mal FFT von Hand auszulösen. Wenn FFT als Funktion platziert werden könnte entlang des Eingangsvektors, dann wäre das die gewünschte Lösung. Warum rechnet FFT nicht automatisch, wie andere Funktionen auch? Oder gibt es das vielleicht doch?

    Antworten

  8. Danke für die Anleitung!
    Wenn man Messergebnisse als Amplitudenspektrum hat bzw die Darstellung im Frequenzbereich, gibt es mit Excel auch eine Möglichkeit eine inverse FFT durchzuführen? Um so das originale Signal im Zeitbereich zu erhalten?

    Antworten

    1. Hi Jörg, danke dir!
      Ja, das war mir wichtig, weil in vielen Tutorials wird irgendwo gestartet, wo man gar nicht versteht, was da los geht.
      Der Nachteil ist, dass Leser die schon etwas Ahnung haben, überblättern und zu spät wieder einsteigen.

      Antworten

  12. Hallo,

    Danke, sehr gut aufbereitet! Es hat mir sehr weitergeholfen DFT zu verstehen. Ich möchte aber jetzt einen Schritt weiter gehen und das Signal aus den Frequenzkomponenten rekonstruieren (IDFT) . Frequenz und Amplitude wurden ja ermittelt, aber wie bekommt man die Phase?

    Antworten

  13. An excellent method, but can you put it in english.

    I just need to know what Rauschen mean in english in more technical term

    A great input to my study….

    Antworten

  14. In einem Video wird davon gesprochen, dass das Amplitudenspektrum dem Realteil des komplexen Amplitudenspektrums entspricht (also der Realteil der Komplexen Zahl der FFT). In Excel allerdings wird der Betrag der Komplexen Zahl berechnet (Befehl IMABS())
    Was ist jetzt richtig? Bzw. was sagt mir der Real- bzw. Imaginärteil der Komplexen Zahl die der FFT-Algorithmus in Excel ausgibt?

    Antworten

  16. Gemäss “Fouriertransformation für Fussgänger” von Prof. Dr. Tilman Butz macht die FFT “automatisch die Annahme, dass {fk} außerhalb des Intervalls [Anmerkung: des gesampelten Intervalls T = Nt] periodisch fortgesetzt wird. Wenn N=256, dann muss f257 beim Beispiel also die gewählte Sinusschwingung mit einer vollen Periode beenden. T257 muss folglich ein Vielfaches der Periode T der Hauptschwingung des gesampelten Intervalls sein und – um beim Beispiel zu bleiben – 0 sein, weil f0 = 0 ist. Wenn im Beispiel die Abtastfrequent zur Illustration auf 50.196078431 Hz erhöht wird, ist obige Bedingung erfüllt und eine FFT zeigt dann haargenau die Frequenz von 10 Hz mit der Amplitude von 1. Natürlich ist es unmöglich, in Voraus zu wissen, was die Abtastfrequenz sein muss, damit 256 Samples – oder irgendeine Anzahl Samples in der Anzahl 2x (lese: 2 hoch x) – das Kriterium der exakten periodischen Fortsetzung der Schwingung im gesampelten Intervall erfüllt.
    Um beim Beispiel zu bleiben: Wird die Abtastfrequenz von 50 Hz beibehalten, wird das Kriterium erfüllt, wenn die Frequenz der Sinusschwingung 10.15625 Hz ist. Die Excel FFT zeigt dann haargenau die Frequenz von 10.15625 mit der Amplitude von 1 (solange kein Rauschen beigemischt wird). Alle anderen Frequenzen haben dann perfekt die Amplitude 0.
    Das zufällige Abschneiden der im Sampling Intervall vorherrschenden Schwingungen («bei mehreren spektralen Schwingungen schneidet man immer irgendeine Komponente im falschen Zeitpunkt ab») ist also problematisch. Dem könnte mit dem so genannten «Zero-padding» begegnet werden.
    (Ich entschuldige mich: In der Antwort können leider Indices nicht tiefgestellt und Potenzen nicht hochgestellt werden. Das Delta beim delta t wird als kleines Rechteck dargestellt. Hoffe, das Obiges trotz dieser Umstände verständlich bleibt.)

    Antworten

Leave a Reply

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert