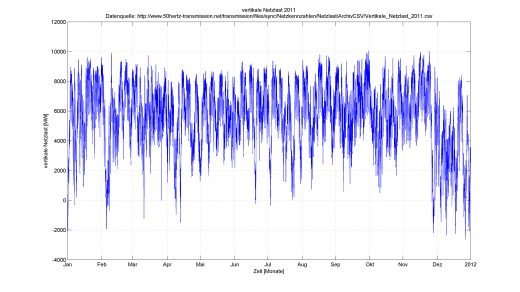
Um technische Sachverhalte beurteilen zu können, bietet es sich an, diese erst einmal zu messen. Die physikalische Größe wird also vom Computer diskret (d.h. nur “alle paar Millisekunden” oder “1x im Jahr” oder “jede 15min”) abgespeichert und kann dann weiter verarbeitet werden. Beispielhaft hier die vertikale Netzlast des deutschen Stromnetzes von 2011:
Möchte man dieses gemessene Signal jetzt auf beinhaltende Frequenzanteile untersuchen, so wurde vom genialen und zu seiner Zeit verkannten Mathematiker Joseph Fourier, die nach ihm benannte Fourier-Analyse entwickelt, welche das exzellent erledigt.
Genau genommen ist die Fourier-Analyse eher ein mathematisches Gebilde, welches für kontinuierliche Signale eine geschlossene Lösung ergibt. Mit dem Computer können aber keine kontinuierlichen Signale abgespeichert werden, weshalb eigentlich immer die diskrete Fourier Transformation (DFT) gemeint ist.
Diskrete Fourier Transformation
Dies lässt sich mit Matlab relativ einfach bewerkstelligen:
Y = fft(Signal)
Doch so einfach ist das dann nicht, man muss nämlich ganz schön aufpassen, damit man zu den berechneten Werten Y auch eine zugehörige Frequenz bekommt. Denn das ist ja der Sinn der Fourier-Transformation, dass man ein Signal in den Frequenzbereich transformiert.
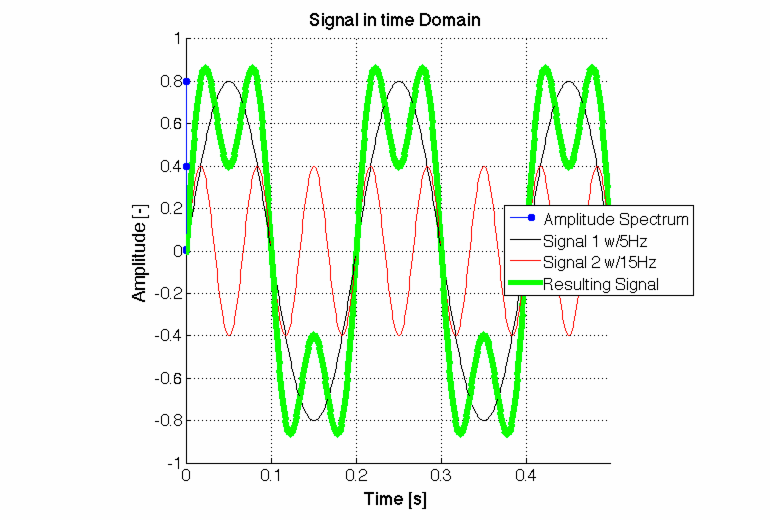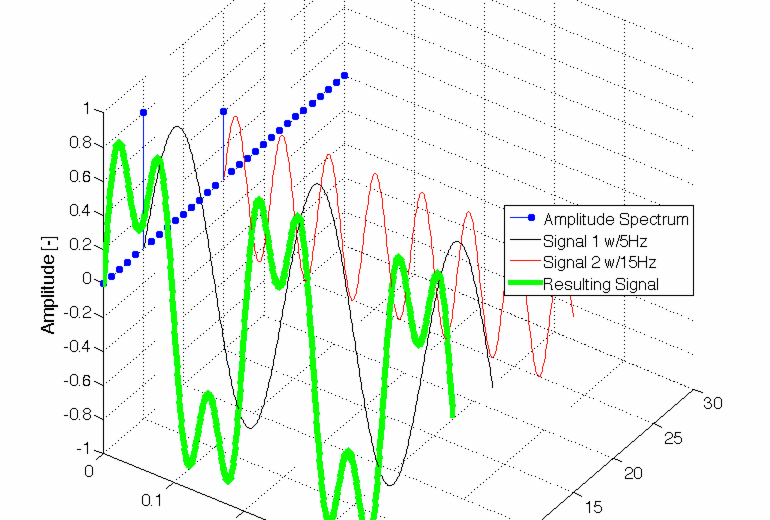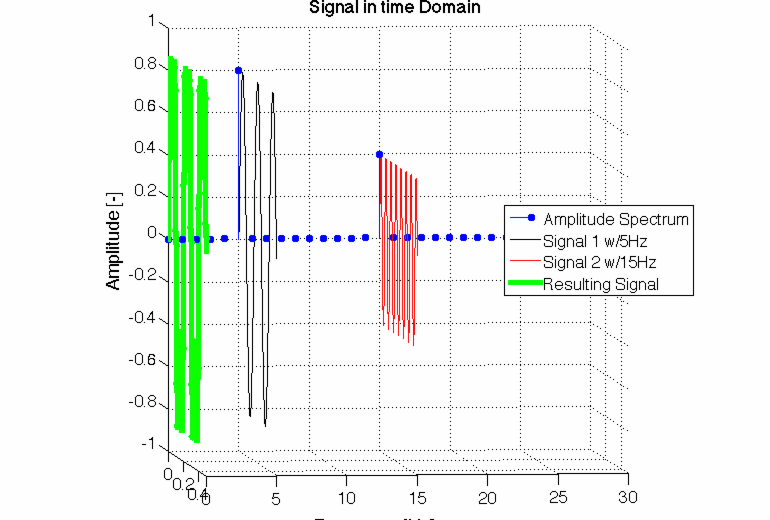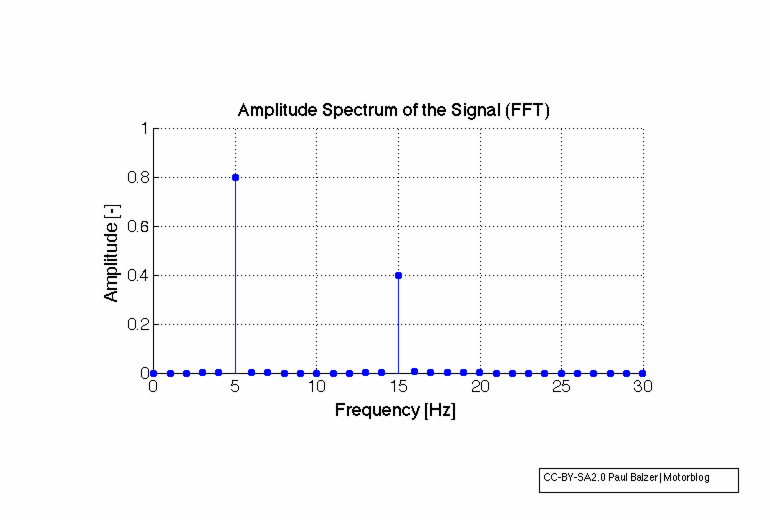
CC-BY-SA2.0
Matlab-Code zur Berechnung der FFT bzw. DFT
%% FFT der vertikalen Netzlast
clear all; close all; clc
% Datenquelle:
% http://www.50hertz-transmission.net/transmission/...
% files/sync/Netzkennzahlen/Netzlast/ArchivCSV/...
% Vertikale_Netzlast_2011.csv
filedata = importdata('Vertikale_Netzlast_2011.csv',';');
dt = 15; %min Abtastintervall
dh = 60/dt;%Stundenteiler
P = filedata.data; %vertikale Netzlast in MW
t = 0:dt:(dt*length(P)-1); t=t';%Zeit in min
thour = t./(dh*dt);
tday = thour./24;
tweek = tday./7;
plot(tday,P)
grid on
xlim([0 364])
set(gca,'XTick',[0 31 59 90 120 151 181 212 242 273 303 334 364])
set(gca,'XTickLabel',{'Jan', 'Feb','Mar','Apr','Mai','Jun','Jul',...
'Aug','Sep','Okt','Nov','Dez','2012'})
xlabel('Zeit [Monate]')
ylabel('vertikale Netzlast [MW]')
title([{'vertikale Netzlast 2011'};{'Datenquelle: http://www.50hertz-transmission.net/transmission/files/sync/Netzkennzahlen/Netzlast/ArchivCSV/Vertikale\_Netzlast\_2011.csv'}])
set(gcf,'PaperPositionMode','Auto','Position',[100 100 1280 720])
print('-dpng','-r300','vertikale-Netzlast.png')
Y=fft(P); %Frequenzspektrum der vertikalen Mittellast berechnen
Y(1)=[]; %erster Wert ist Gleichanteil (Mittelwert)
n = length(P);
amplitude = abs(Y(1:floor(n/2))).^2;
nyquist = 1/2;
freq = (1:n/2)/(n/2)*nyquist*dh;
period=1./freq;
figure(2)
semilogx(period,amplitude,'LineWidth',2);
grid on
xlim([1 1000])
xlabel('Periodendauer [h]')
title([{'Frequenzspektrum der vertikalen Netzlast für das Jahr 2011'};{'Datenquelle: http://www.50hertz-transmission.net/transmission/files/sync/Netzkennzahlen/Netzlast/ArchivCSV/Vertikale\_Netzlast\_2011.csv'}])
set(gcf,'PaperPositionMode','Auto','Position',[100 100 1280 720])
set(gca,'XTick',[1:10,20:10:80,100:100:500,1000])
text(12,2e14,'12h \rightarrow','HorizontalAlignment','right','FontSize',18)
text(24,3e14,'24h \rightarrow','HorizontalAlignment','right','FontSize',18)
text(84,0.5e14,'84h 15min \rightarrow','HorizontalAlignment','right','FontSize',18)
text(168,2.5e14,'168h 30min \rightarrow','HorizontalAlignment','right','FontSize',18)
print('-dpng','-r300','vertikale-Netzlast-FFT.png')
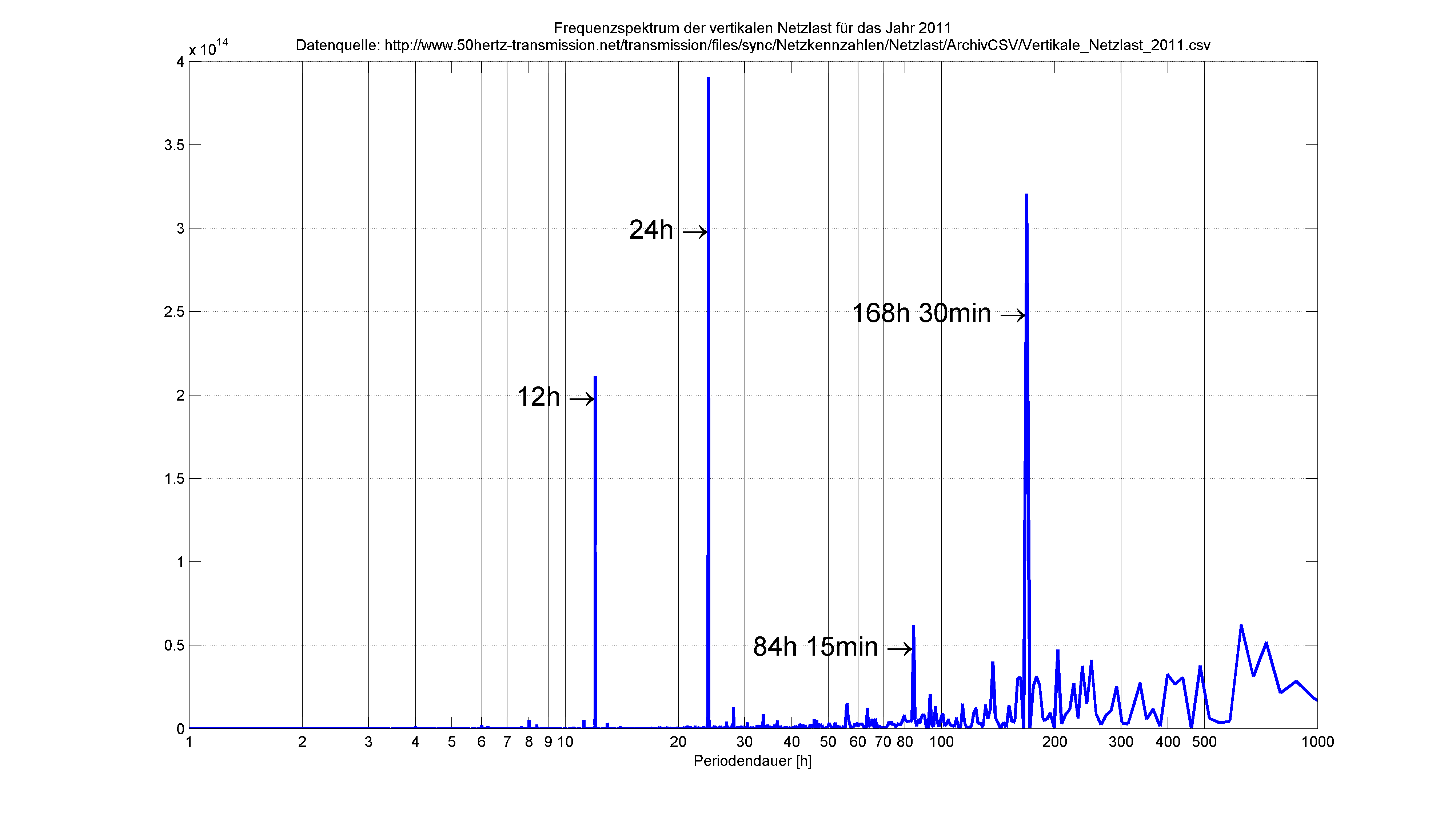
erzeugt das Frequenzspektrum des Signals:
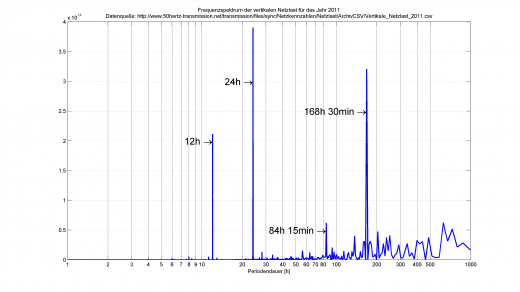
Frequenzspektrum der vertikalen Netzlast aus dem Jahr 2011, Datenquelle: http://www.50hertz.com/de/149.htm






6 Comments