Beim Fahren muss der Reifen eine Kraft auf die Fahrbahn übertragen. Im Allgemeinen eine Mischung aus Längs- und Querkraft, im Speziellen nur eine Längskraft (Beschleunigen & Bremsen). Die übertragbare Längskraft hängt maßgeblich von der in Richtung Boden drückenden Gewichtskraft ab. Umso mehr Gewichtskraft nach unten drückt, desto mehr Längskraft kann der Reifen übertragen.
Als relatives Maß wird der Reibkoeffizient µ verwendet, welcher angibt, wieviel Längskraft im Verhältnis zur Normalkraft übertragen wird.
Der Reibkoeffizient µ ist allerdings nicht konstant. Er hängt unter anderem vom Schlupf ab.
Radschlupf S
Bei vollständig durchdrehenden Rädern ist der Schlupf 100%, bei stillstehenden Rädern oder bei konstanter Fahrt (Fahrzeuggeschwindigkeit und Reifenumfangsgeschwindigkeit sind identisch) ist der Schlupf 0%. Formelmäßig definiert ist der Schlupf mit:
Damit ergibt sich bei einer Fahrgeschwindigkeit von 50km/h (vfzg) folgender Wert für den Radschlupf.
µ-Schlupf-Kurve
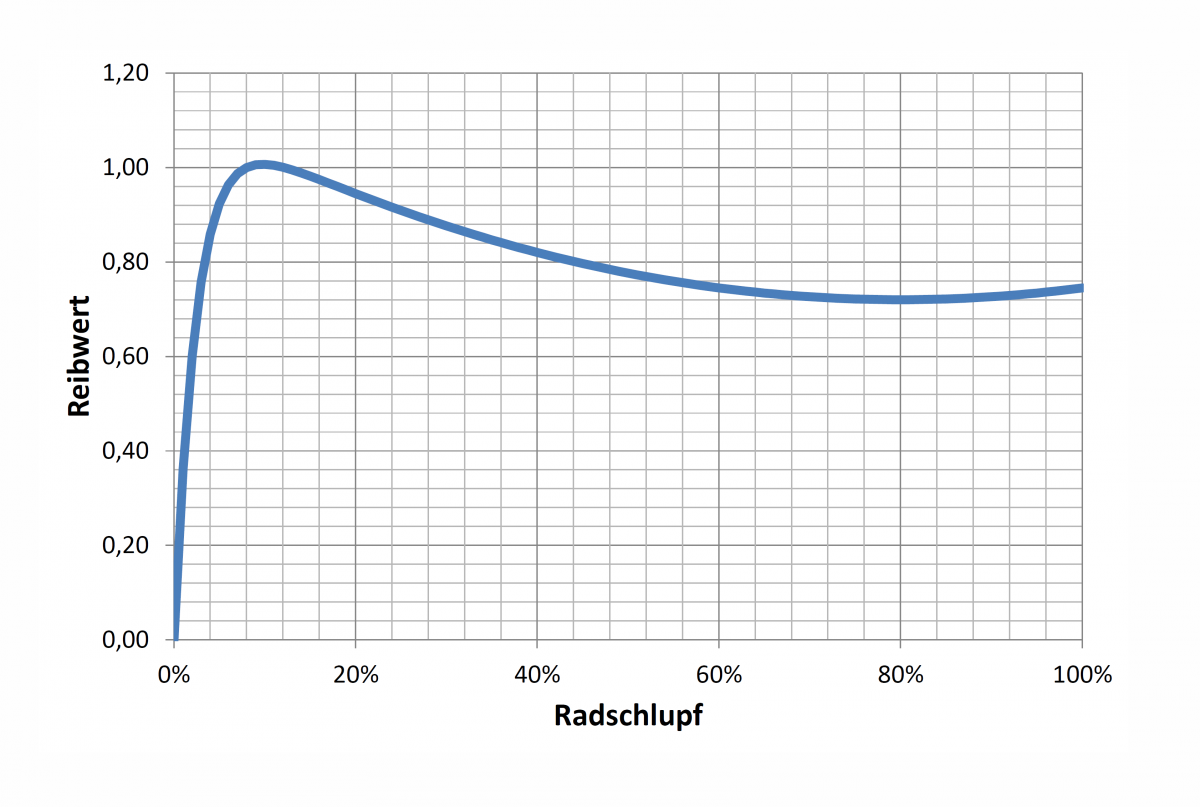
Die Abhängigkeit von übertragbarer Kraft (hohe Beschleunigung) und Schlupf ist in vielen mathematischen Modellen beschrieben. Ein einfaches und relativ weit verbreitetes Modell ist die so genannte “Magic Formula” von Pacejka, welche die µ-S-Kurve nachfolgen modelliert:
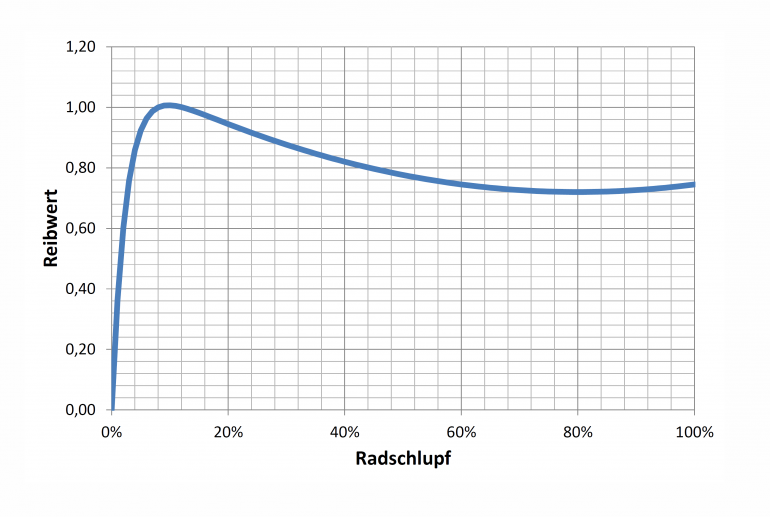
Es ist zu sehen, dass die maximale übertragbare Kraft, welche das Fahrzeug beschleunigt, nicht bei völlig durchdrehenden Rädern erreicht wird, sondern bei (je nach Reifen/Fahrbahn) ca. 5…20% Radschlupf.
Pacejkas Magic Formula
mit
wobei S nur zwischen 0…1 variieren darf.
Durch Variation der Parameter A, C, D, n, K und d kann die Kurve beliebig angepasst werden, sodass das korrekte Reifenmodell abgebildet werden kann.
Matlab m-file zur Berechnung
Mit Hilfe dieses Matlab Scripts wird ein Fenster erzeugt, bei welchem die Parameter frei variiert und angepasst werden können.
% Paceijka Magic Formula für Längsdynamik des Reifens
clear all;
close all;
clc;
% Parameterinitialisierung
A=1.12;
C=0.625;
D=1;
n=0.6;
K=46;
d=5;
% Schlupf
lambda = 0:0.005:1;
% Grafik erzeugen
figure('Name','Pacejka Magic Formula in Längsrichtung')
% Formatierung vorab
grid on
daten = line(0,0,'LineWidth',3);
xlabel('Radschlupf \lambda','FontSize',12);
ylabel('Reibungskoeffizient \mu','FontSize',12);
xlim([0 1])
ylim([0 2])
% Slider erzeugen
% A
Aslider = uicontrol('Style', 'slider',...
'Position', [650 330 140 20],'min',0.5,'max',2,...
'value',1.12,'String','A');
text(1.02,1.9,'A=','FontSize',14)
Awert=text(1.08,1.9,num2str(A),'FontSize',14);
% C
Cslider = uicontrol('Style', 'slider',...
'Position', [650 275 140 20],'min',0.2,'max',1.4,...
'value',0.625,'String','C');
text(1.02,1.55,'C=','FontSize',14)
Cwert=text(1.08,1.55,num2str(C),'FontSize',14);
% D
Dslider = uicontrol('Style', 'slider',...
'Position', [650 220 140 20],'min',0.2,'max',1.4,...
'value',1,'String','D');
text(1.02,1.2,'D=','FontSize',14)
Dwert=text(1.08,1.2,num2str(D),'FontSize',14);
% n
nslider = uicontrol('Style', 'slider',...
'Position', [650 165 140 20],'min',0.4,'max',2.0,...
'value',0.8,'String','n');
text(1.02,0.85,'n=','FontSize',14)
nwert=text(1.08,0.85,num2str(n),'FontSize',14);
% K
Kslider = uicontrol('Style', 'slider',...
'Position', [650 110 140 20],'min',10,'max',180,...
'value',46,'String','K');
text(1.02,0.5,'K=','FontSize',14)
Kwert=text(1.08,0.5,num2str(K),'FontSize',14);
% d
dslider = uicontrol('Style', 'slider',...
'Position', [650 55 140 20],'min',1,'max',20,...
'value',5,'String','d');
text(1.02,0.15,'d=','FontSize',14)
dwert=text(1.08,0.15,num2str(d),'FontSize',14);
% Plot ausrichten und Größe festlegen
set(gcf,'Position',[100 100 800 400])
set(gca,'Position',[0.1 0.15 0.7 0.8])
while(1)
A = get(Aslider,'value');
C = get(Cslider,'value');
D = get(Dslider,'value');
n = get(nslider,'value');
K = get(Kslider,'value');
d = get(dslider,'value');
%Magic Formula zur Berechnung der µ-Schlupfkurve der Reifenlängsdynamik
B = (K/d)^(1/n);
mu = sign(lambda).*(A.*(1-exp(-B*abs(lambda)))+C*lambda.^2-D*abs(lambda));
set(daten,'xdata',lambda,'ydata',mu);
set(Awert,'string',num2str(A))
set(Cwert,'string',num2str(C))
set(Dwert,'string',num2str(D))
set(nwert,'string',num2str(n))
set(Kwert,'string',num2str(K))
set(dwert,'string',num2str(d))
drawnow
end
erzeugt



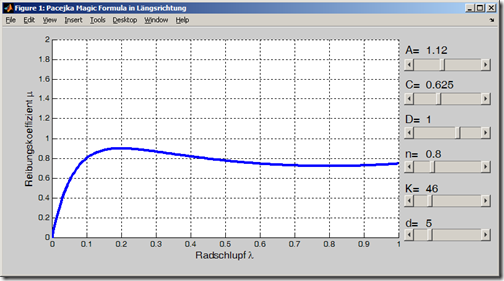


4 Comments
Hallo,
können sie mir auf die Schnelle erklären, wofür die Parameter A, C, D, n, K und d stehen?
Ich kenne die Magic Formula nur mit anderen Kürzeln.
Vielen Dank!
Viele Grüße
Linus
Sorry, was hier steht ist technisch leider ziemlicher Mumpitz, speziell was dieses Diagramm betrifft.
Der Haftreibungskoeffizient der Materialpaarung Asphalt-Gummi ist irgendwo bei 0,7-0,9, je nach Quelle.
Google und Co hilft, z.B.: willkürlich eine Quelle https://www.schweizer-fn.de/stoff/reibwerte/reibwerte.php
Bezogen auf das Diagramm heißt das, dass der Reibkoeffizient schon bei Radschlupf 0 irgendwo größer 0,7 starten müsste und nicht so wie hier falsch dargestellt bei Radschlupf 0 der Reibkoeffizient ebenfalls 0 sei.
Viele Grüße