Im Schulunterricht steht oft eine Funktion f(x) zur Verfügung, welche symbolisch integriert werden kann (Stammfunktion bilden) und dann das bestimmte Integral in den Grenzen berechnet wird. Im Alltag des Ingenieurs ist das eher selten der Fall. Der wesentlich häufigere Fall ist, dass bestimmte Messwerte numerisch integriert werden müssen. Sei es in Excel oder auf einem Steuergerät (Mikrocontroller).
Als Beispiel soll die von einem Beschleunigungssensor gemessene Längsbeschleunigung eines Fahrzeugs dienen. Gesucht ist die Fahrzeuggeschwindigkeit.
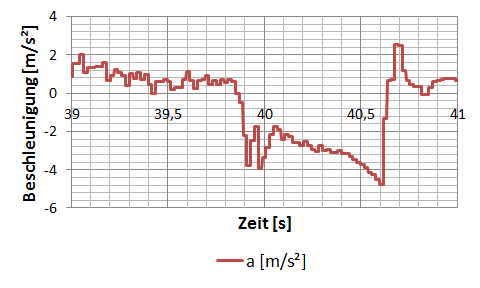
Der mathematische Zusammenhang zwischen Beschleunigung und Geschwindigkeit ist klar: Integration über der Zeit. Doch wie kann man das Problem mit Excel (oder jeder anderen Tabellenkalkulation) lösen, wenn gar keine Funktion a(t) zur Verfügung steht, welche man dann symbolisch integrieren kann?
Numerische Integration
Das Zauberwort heißt numerische Integration. Sie läuft auf jedem Taschenrechner, auf jedem Computer und auf jedem Mikrocontroller und kann eine sehr gute Lösung sein. Um unnötig Text zu vermeiden soll an dieser Stelle auf die grandiose Erklärung von Prof. Loviscach verwiesen werden:
Zurück zum Beispiel: Die aktuelle Beschleunigung a(t) steht nicht als kontinuierliche Funktion zur Verfügung, sondern wird diskret (d.h.: „nur alle paar Millisekunden“) ermittelt. Dies z.B. durch einen A/D Wandler, Datenübertragung durch einen CAN-Bus oder Verarbeitung durch Mikrocontroller. Eine weitere Möglichkeit ist auch, dass die Daten in einer Messwertedatei (z.B. Excel Datei) gespeichert sind und zur nachträglichen Offlineauswertung herangezogen werden.
Trapezverfahren
Ein Verfahren, welches einen guten Mittelweg zwischen einfacher Anwendung und Genauigkeit bietet, ist das Trapezverfahren. Auch hierzu soll auf Prof. Loviscach verwiesen werden, welcher das Verfahren ausgezeichnet erläutert:
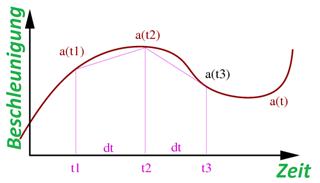
Dabei wird sich zu Nutzen gemacht, dass die Integration auch „die Fläche unter der Kurve“ darstellt und somit die Fläche durch Trapeze angenähert werden kann. Die Formel zur numerischen Integration kann mit nachfolgender Abbildung einfach gefunden werden.
\(v_{t2}=v_{t1}+\left(\frac{a(t_1)+a(t_2)}{2}\right)\cdot(t_2-t_1)\)Berechnung in Excel
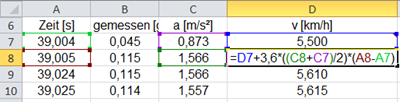
Die Berechnung in Excel läuft nun folgendermaßen ab:
Die Geschwindigkeit zu Beginn (v0) muss bekannt sein (Anfangswertproblem).
Es kann gezeigt werden, dass die numerische Integration mittels Trapezmethode für Polynome 1. Grades (also Geraden) exakt rechnet. Die Messwerte in einer Tabellenkalkulation werden mit diesem Verfahren ebenfalls exakt integriert.
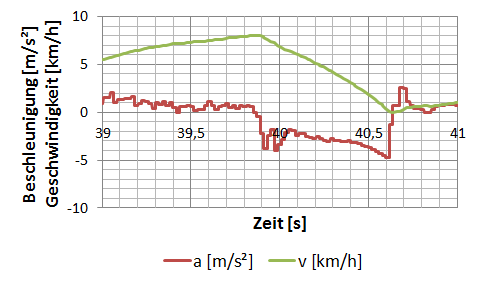
Die Integration der Beschleunigung ergibt für das verwendete Beispiel folgenden Geschwindigkeitsverlauf, wenn als Ausgangsgeschwindigkeit v0 = 5.5 km/h angenommen wird.
Pro Tipp
Wenn gar nicht der Verlauf des integrierten Wertes benötigt wird (grüne Kurve im Diagramm oben), sondern nur ‘der Flächeninhalt unter der Kurve’, dann kann man auch einfach
=MITTELWERT(Beschleunigungen) * (Endzeit - Anfangszeit)
rechnen.




19 Comments
Kann/darf V0 = 0 sein? Also die Anfangsgeschwindigkeit = 0? Macht ja Sinn wenn es vom Stillstand losgeht.
Danke und Grüße
Natürlich
Warum rechnest du den Offset 0,044 drauf?
Weil der Sensor nicht ganz exakt horizontal eingebaut war und in Ruhelage 0.044 misst statt 0.
Genau das was ich gesucht hab. Vielen Dank!
Hallo,
sehr schöne Seite. Kurze Frage zu der Excel-Berechnungsformel: warum ist der Faktor 3,6 dort enthalten?
Viele Grüße
Florian
Umrechnung m/s zu km/h
okay, hab es gerade selber herausgefunden. Es ist der Umrechnungsfaktor von m/s nach km/h.
Grüße
Florian
wie hast du dann die Abbildung mit den Trapezen gemacht?
Ich glaube mit Geogebra
unlogisch für mich nicht erklärbar
super seite, danke!
Vorab: die Erklärung sowie das Beispiel sind hervorragend zum Nachvollziehen!!! Ich beabsichtige durch meine Messwerte für die Beschleunigung zum Weg s(t) zu gelangen. Hierfür muss ich von der Beschleunigung a(t) integrieren zur Geschwindigkeit v(t) und v(t) integrieren zum Weg s(t). Wäre es theoretisch denkbar, dieselbe Vorgehensweise analog von v(t) auf s(t) anzuwenden? bzw. wie würden die Anfangswerte für s(t) festliegen?
Ja, das funktioniert natürlich! Man hat allerdings das Problem, dass man auch das “Rauschen” und die Nullpunktabweichung des Beschleunigungssensors mit aufintegriert und damit wird das Ergebnis nicht unbedingt genau. Für einen kurzen Zeitraum mag das funktionieren.
Der Weg s(t=0) ist beliebig, z.B. 0m oder jeder andere Wert.
Hallo Paul, eine allgemeine Frage zum Verständnis: wenn ich eine Beschleunigung habe völlig irrelevant ob sie schneller oder langsamer wird, kann meine Geschwindigkeit ja nicht negativ werden, es sei denn ich habe eine negative Beschleunigung. Was mich aber nun interessieren würde ist, dass der Weg immer ansteigen müsste, da rein logisch gesehen bei Geschwindigkeit > 0 der Weg niemals weniger werden kann. Wie beeinflusst dieser den Weg, wenn die Geschwindigkeit negativ ist? Welche Faktoren könnten dazu führen? Meine Messreihe besteht aus: mg Werten, die ich x*9,81/1000 in [m/s²] berechnen muss. ich habe analog zu deinem Tutorial die V(t) berechnet. Aber die Endwerte für den s(t) werden teils weniger, was für mich keinen Sinn macht. :)