Wer rapid Prototyping betreibt und schnell eine funktionierende Lösung auf die Beine stellen möchte oder muss, der wird an Tinkerforge (hoffentlich) nicht vorbei kommen. In meinen Augen allem Arduino Kram überlegen, besser dokumentiert, besser in jede Software zu integrieren und qualitativ oberste Stufe. Außerdem Open Hardware und Open Source, Made in Germany!
Im Angebot befindet sich neben Laserdistance-Bricklet und IR-Distance Bricklet auch ein Ultraschall Distance Bricklet, welches in der Robotik und vielen anderen Bereichen sicherlich eine wichtige Stellung einnimmt. Typischer Anwendungsfall: Entfernung zu einem Hindernis bestimmen. Verwendet man etwas ausgefeiltere Algorithmen, sollten die Messgrößen in einer Einheit sein, d.h. typischerweise in SI Einheiten.

Es gibt ein Problem: Der Rückgabewert der Bricklets ist nicht in cm oder mm oder m, sondern eine dimensionslose Größe, welche man selbst in Distanz umrechnen muss. Der Tinkerforge Support schreibt:
Das Distance US Bricklet gibt einen ‘Analogwert’ zwischen 0 und 4095 zurück. Der Rückgabewert ist nicht in cm oder mm oder ähnliches. Wir können dort leider nicht einfach eine Lookup-Table einbauen und direkt eine Entfernung zurückgeben (wie wir es z.B. bei dem Distance IR machen), da der Ausgabewert bei dem Ultraschallsensor extrem von der Versorgungsspannung abhängt. Diese ist aber leider bei jedem PC/Hub ein bisschen anders. D.h., wenn ihr das Distance US Bricklet nutzen wollt um Entfernungen in cm/mm zu messen, müsst ihr euch selber eine Lookup-Table bauen dafür.
Let’s do it…
Quantisierung
Der analoge Rückgabewert des Ultraschallsensors wird offensichtlich mit 12bit quantisiert, d.h. \(2^{12}=4096\) verschiedene digitale Rückgabewerte, mit welchen der Messbereich aufgeteilt werden muss. Der Messbereich ist laut Datenblatt 2cm…400cm. Diese Informationen führen offensichtlich zu folgender linearer Gleichung:
\[d [cm] = \frac{398cm}{4096} \cdot i + 2cm\]
wobei \(i\) der rohe Rückgabewert des Ultraschall Bricklets ist.
Nichtlinearität
Nun zeigt es sich allerdings, dass die Gleichung nicht korrekt/vollständig ist. Es ist noch ein Faktor \(k(i)\) zu bestimmen, welcher die Nichtlinearität des US Bricklet abfängt. Die vollständige Gleichung ist
\[d [cm] = k(i) \cdot \frac{398cm}{4096} \cdot i + 2cm\]
Die Frage ist, wie lautet die Funktion \(k(i)\)? Diese ist abhängig von der Versorgungsspannung, was allerdings hier nicht mit betrachtet wurde! Hier wird von konstanter Spannung ausgegangen und nur ein LookUp Table für einen Rechner erstellt.
Versuchsaufbau zur Bestimmung der Entfernung
Der Versuchsaufbau ist folgendermaßen: US-Bricklet und Laserdistance-Bricklet direkt nebeneinander angeordnet und mit Tinkerforge DataLogger die Werte aufgezeichnet. Die ‘wahre Entfernung’ kommt vom Laserdistance-Bricklet und dient als Sollwert.

Versuchsaufbau: Tinkerforge Laserdistance und Ultraschall Sensoren direkt nebeneinander zur Besimmung der Entfernung zu einer Wand
Nun wurde Schrittweise zwischen 10cm…280cm der Abstand erhöht und über einen Zeitraum von mehreren Minuten der Rohwert des Ultraschallsensors geloggt. Beim Vergleich zwischen den RAW Werten des Ultraschallsensors und dem wahren Wert vom Laserdistance-Bricklet, ergab sich ein nichtlinearer Zusammenhang. Diese Funktion muss bestimmt werden.
Bestimmung der Funktion
Um die RAW Werte auf die korrekte (=Laserscanner) Entfernung zu skalieren, muss der Faktor \(k\) in Abhängigkeit des RAW Wertes \(i\) bestimmt werden. Dieser wurde empirisch ermittelt.

Genau genommen kann man einfach in kleinen Schritten den Faktor durch probieren und den MeanSquareError zur wahren Entfernung bestimmen. Der Wert \(k\), der den MSE minimiert, ist der korrekte für die jeweilige Entfernung.
import numpy as np
import pandas as pd
ks = np.linspace(0.0, 1.0, 1000)
x=[]
y=[]
for d in distances:
logfile = 'log%icm.csv' % d
data = pd.read_csv(logfile, sep=';')
error={}
for k in ks: # Let's Bruteforce it
d_ist = k*(398.0/4096.0)*data['RAW'].median() + 2
error[k] = (d_ist - d)**2.0
# Listen füllen mit
x.append(data['RAW'].median()) # Distance RAW Wert
y.append(min(error, key=error.get)) # k mit geringsten MSE
Mit den Werten aus den Listen x und y kann man nun eine polynomiale Funktion anpassen, welche die Messwerte am besten widerspiegelt. Dabei ist auf eine Balance zwischen möglichst passender Beschreibung und Overfitting zu achten. Ein Polynom 4. Grades scheint ein guter Kompromiss zu sein. Der Sollwert [4095, 1] wurde noch manuell eingefügt.
# Polynom fitten z = np.polyfit(x, y, 4) i_range = np.linspace(0, 4095.0, 4096) k = np.poly1d(z) plt.scatter(x, y, s=100, alpha=0.6, label='Messungen') plt.plot(i_range, k(i_range), label='Polynom')
Über alle gemessenen Entfernungen ergibt sich folgende Funktion:
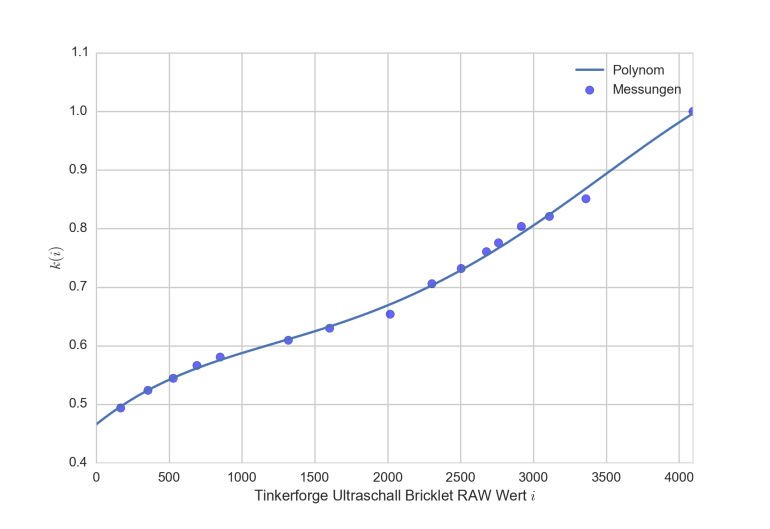
Raw-Werte i des Tinkerforge Ultraschall Bricklets für verschiedene Entfernungen und entsprechender Faktor k(i), welcher mit der Formel diesen Wert optimal auf die wahre Entfernung umrechnet
Die Faktoren des Polynoms sind
array([ -4.60578246e-15, 4.35156579e-11, -1.18489660e-07, 2.01430169e-04, 4.65647198e-01])
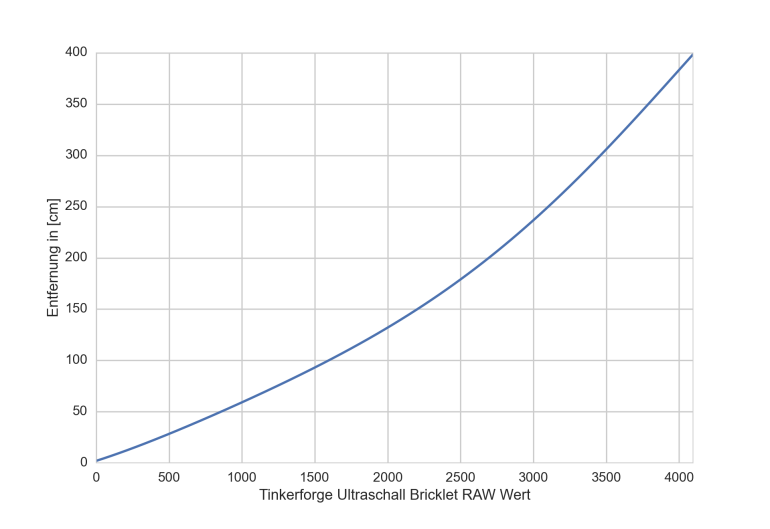
Damit lässt sich die Formel nun komplett berechnen und ein Lookup-Table für die Tinkerforge Ultraschall Bricklet RAW Werte zu korrekter Entfernung in cm bestimmen.
Lookup-Table
Ein Lookup-Table für den Tinkerforge Ultraschall-Bricklet könnte so aussehen, ist allerdings von der Spannungsversorgung extrem abhängig, könnte also bei jedem Rechner/RaspberryPi/USB Port etwas anders sein. Im konkreten Fall hat es sich sogar gezeigt, dass ein Ansteigen der Prozessorlast am Laptop eine minimale Änderung der Versorgungsspannung des USB Ports erzeugte, was ‘Sprünge’ in der Entfernung zur Folge hat.
z = np.array([ -4.60578246e-15, 4.35156579e-11, -1.18489660e-07,
2.01430169e-04, 4.65647198e-01])
k = np.poly1d(z)
# CSV schreiben
print('RAW,Distance[cm]')
for i in i_range:
print('%i,%.1f' % (i, k(i)*(398.0/4096.0)*i+2))
# Python Dictionary erzeugen
lookuptable={}
for i in i_range:
lookuptable[i]=k(i)*(398.0/4096.0)*i+2
Nun kann für jeden RAW Wert eine physikalische Entfernung berechnet werden.
In [1]: lookuptable[300] Out[1]: 17.057628309828651
Ergebnis
Ohne Gewähr! Bei jeder Versorgungsspannung anders!
Statistische Aussagen
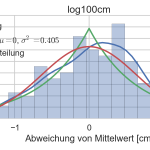
Ein paar Anmerkungen zur quantitativen statistischen Analyse der Sensormesswerte. In den meisten Robotik-Anwendungsfällen werden Sensormesswerte als AWGN Signal (additive white gaussian noise) modelliert. Das bedeutet, dass der Sensor den wahren Wert + ein normalverteiltes Rauschen als Messwert widergibt. Ein gutes Beispiel ist das Kalman Filter, welches von normalverteilten Messungen ausgeht. Die Messungen ergaben, dass diese Annahme nur in einem Messbereich zwischen \(d=1…2m\) erfüllt ist.
- Histogramm der Messwerte bei 1m Entfernung zum Hindernis mit Wahrscheinlichkeitsdichte (blau), Normalverteilung (rot) und Laplace Verteilung (grün)
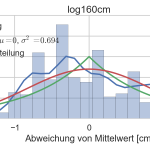
- Histogramm der Messwerte bei 1,6m Entfernung zum Hindernis mit Wahrscheinlichkeitsdichte (blau), Normalverteilung (rot) und Laplace Verteilung (grün)
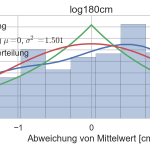
- Histogramm der Messwerte bei 1,8m Entfernung zum Hindernis mit Wahrscheinlichkeitsdichte (blau), Normalverteilung (rot) und Laplace Verteilung (grün)






One Comment