Im ersten Teil der Robotik-Sensor Reihe, wurde ein Look-Up Table für den Tinkerforge Ultraschall Sensor parametriert. Nun ist es möglich reale Entfernungen von diesem Sensor zu erhalten. Der Beitrag schloss mit den Worten, dass eine Normalverteilung für Sensorwerte nur im Bereich 1…2m anzunehmen ist. Etwas fortgeschrittene Filterverfahren, wie das Kalman Filter, arbeiten unter der Annahme, dass die Sensoren ein AWGN (Additive White Gaussian Noise) Signal ausgeben. Dies bedeutet, dass der Sensor den wahren Wert zwar messen kann, aber durch zahlreiche Fehlereinflüsse zusätzlich weißes Rauschen aufaddiert mit ausgegeben wird.
Wie nun also den ‘Wahren Wert’ erhalten?
Einfaches Modell: Normalverteilt um den Wahren Wert
Die ernüchterndste Aussage eines jeden Messtechnikers ist und bleibt, egal wie genau sein Messverfahren ist, dass der Wahre Wert™ unbekannt ist. Der Sensor versucht lediglich den Wahren Wert geeignet ist Spannung oder Strom umzusetzen. Je nachdem wie geeignet das Messverfahren ist, kommt dies dem Wahren Wert sehr nahe.
Am Beispiel des Tinkerforge Ultraschallsensors zeigt sich das ganz deutlich. Beispielsweise wird dieser in ca. 1 Meter Entfernung vor einer weißen Wand aufgestellt und misst 5min lang die Entfernung. Man erwartet, dass der Sensor 5min lang 1m als Messwert ausgibt. Denn das ist ja der Wahre Wert. Dem ist nicht so. Hier zeigt sich sehr schön die AWGN Annahme. Ein Histogramm für alle Messwerte über 5min sieht so aus:
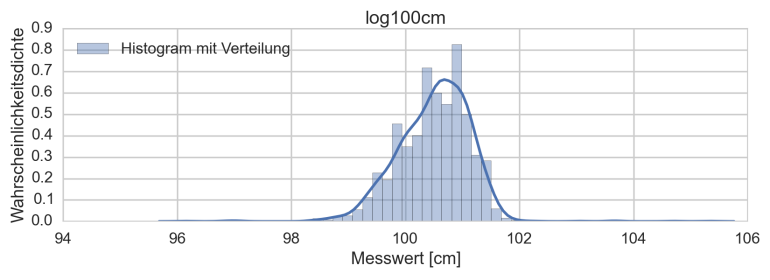
Zieht man den Mittelwert ab und legt eine Gauss-Normalverteilung über dieses Histogramm, ergibt sich folgende Abbildung:
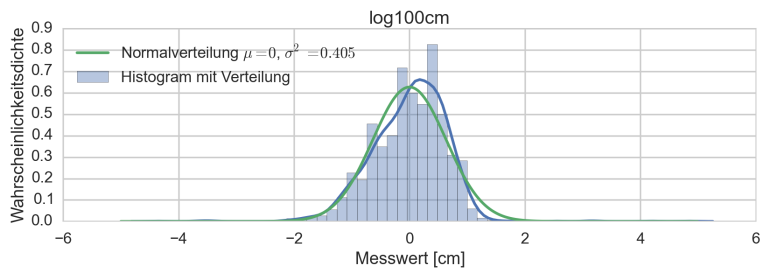Das Sensormodell für diese Entfernung lässt sich sehr gut modellieren mit der mathematischen Formulierung
\[Y_i = X_i + Z_i\sim \mathcal{N}(X_i, N)\]
was nichts anderes bedeutet, dass der Sensorwert \(Y\) zum Zeitpunkt \(i\) zusammengesetzt ist aus dem Wahren Wert \(X\) + einem normalverteilten Sensorrauschen mit Mittelwert um den Messwert und Varianz \(N\). In Python würde man das in etwa so berechnen.
import numpy as np import matplotlib.pyplot as plt mu, sigma = 0., np.std(data['ultraschall_distance_cm']) # in data sind die Messwerte x = np.arange(-5., 5., .01) std = (1/(sigma * np.sqrt(2 * np.pi)) * np.exp(-(x - mu)**2 / (2 * sigma**2))) plt.plot(x, std, label=r'Normalverteilung $\mu=%.0f$, $\sigma^2=%.3f$' % (mu, sigma**2.0))
Es zeigt sich, dass diese einfache Annahme für den Tinkerforge Ultraschall Sensor (und alle anderen Ultraschallsensoren) bei Entfernungen von über 2m nicht mehr ausreichend ist. Das Histogramm für eine Entfernung von ca. 3,55m (bei 4m maximalen Messbereich) ist nachfolgend dargestellt.
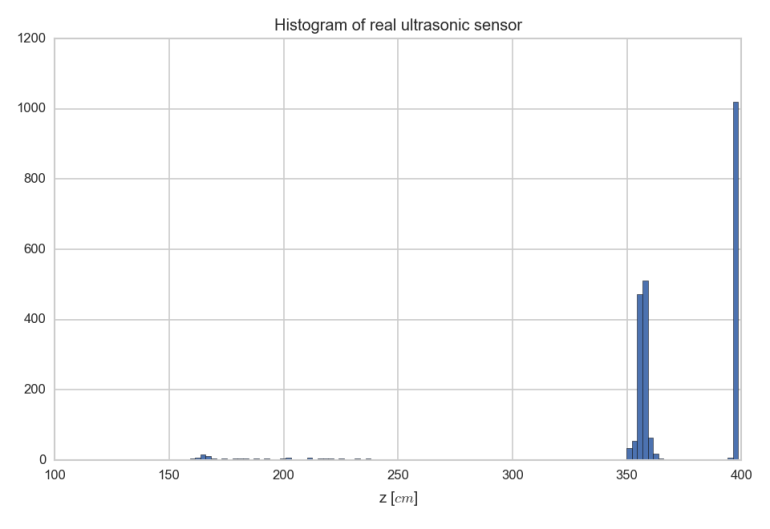
Hier kann man offensichtlich keine Normalverteilung um den Mittelwert mehr fitten. Es muss eine gemischte Dichteverteilung modelliert werden.
Vollständige Modellierung: Gemische Dichteverteilung
Die Sensormodellieren, die im folgenden Vorgestellt wird, geht zurück auf den Großmeister der Robotik, Prof. Sebastian Thrun [Thrun, S. (2000). Probabilistic algorithms in robotics. Ai Magazine, 21(4), 93–109. Retrieved from http://www.aaai.org/ojs/index.php/aimagazine/article/viewArticle/1534].
Ziel der Sensormodellierung
Ziel der Sensormodellierung ist es, ein möglichst korrektes Map eines Raumes oder einer Umgebung zu erfassen, obwohl der Sensor nicht perfekt misst. Es gibt zahlreiche Möglichkeiten, welche den Sensorwert eben nicht korrekt von Sensor bis zur Wand laufen lassen. Diese sollten für eine Kartierung des Raumes probalistisch mit berücksichtigt werden.
Ein schöner Vortrag zur Probalistischen Sensormodellierung kann bei der Uni Freiburg angesehen werden:
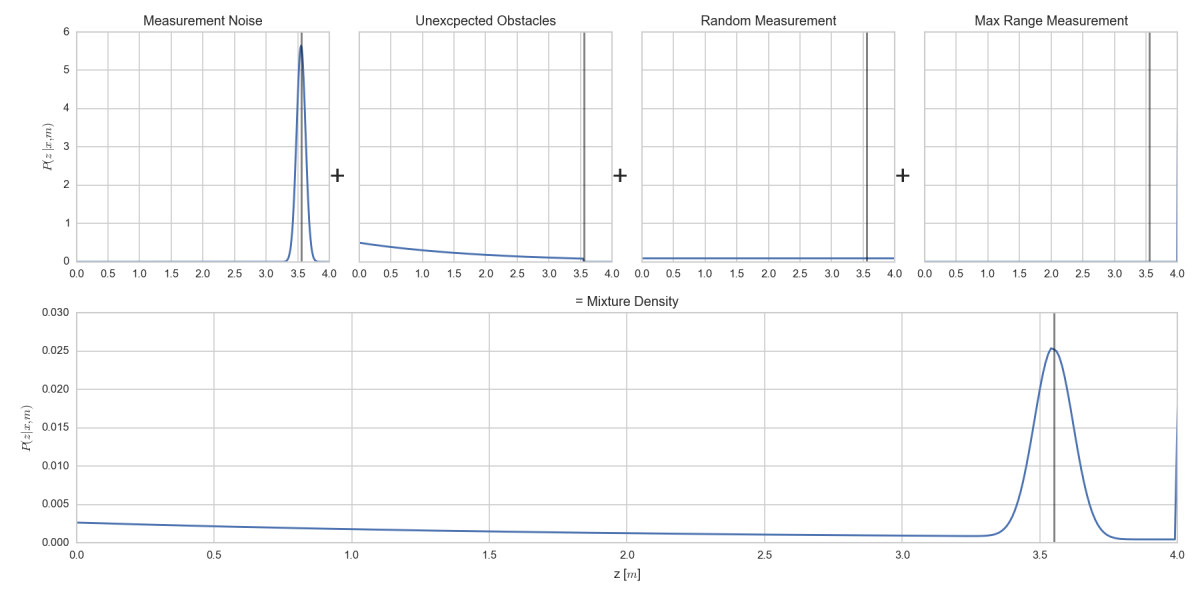
Die Wahrscheinlichkeitsdichte des Sensormesswertes wird zusammengesetzt aus 4 verschiedenen Einzelverteilungen.
\[P(z\mid x,m) = \left(\begin{matrix}P_{hit}(z\mid x,m) \\ P_{unexp}(z \mid x,m) \\ P_{max}(z \mid x,m) \\ P_{rand}(z \mid x,m) \end{matrix}\right)\]
Diese gibt die Wahrscheinlichkeit wieder, dass ein Sensormesswert \(z\) ermittelt wird, bei einer bestimmten Position \(x\) des Sensors in einer bestimmten Welt \(m\). Letzteres bedeutet schlichtweg, dass es eine Wand oder Hindernis in der Welt gibt und der Sensor an einer Position \(x\) vor der Wand steht.
Normalverteilung
Es bleibt die Normalverteilung \(P_{hit}(z\mid x,m)\) um den Wahren Wert mit Normalisierungsfaktor \(\eta\).
\[P_{hit}(z\mid x,m) = \eta \cdot \frac{1}{\sqrt{2 \pi \sigma_z^2}} \cdot \exp{\left(-\frac{1}{2} \cdot \frac{(z-z_{exp})^2}{\sigma_z^2}\right)}\]
Python Code:
varz = 5.0 # Variance zexp = 357.0 # here is the obstacle def Pzx_hit(z): Pzx = 1.0/np.sqrt(2*np.pi*varz) * np.exp(-1/2.0*(z-zexp)**2/varz) eta = np.max(np.sum(Pzx)) return Pzx/eta
Unerwartete Hindernisse
Der Sensor gibt eventuell ein Echo auf ein Hindernis zurück, was sich zwischen dem Sensor und der Wand befindet. Das könnte bei Laserscannern ein Staubkorn oder eine Scheibe sein. Bei Ultraschallsensoren durch die breite Keule etwas, was sich am Rande der Keule befindet und ein Echo erzeugt. Sollte die Umgebung \(m\) in der sich der Roboter befindet nicht statisch sein, so kann mit dieser Komponente auch modelliert werden, dass z.B. ein Mensch o.ä. in den Messbereich zwischen Roboter und Wand läuft. Stehen zwei Hindernisse hintereinander, wird natürlich nur das vordere gemessen. Daher ist es wahrscheinlicher, dass im Nahbereich häufiger Hindernisse auftreten, als im Fernbereich.
\[P_{unexp}(z \mid x,m) = \eta \cdot \lambda \cdot \exp{\left(-\lambda \cdot z\right)}\]
Der Faktor \(\eta\) ist ein Normalisierungsfaktor, welcher das Integral über die entstehende Wahrscheinlichkeitsdichtefunktion auf 1 normiert.
Python Code:
lamb = 0.5 eta = 1.0/(1.0-np.exp(-lamb*zexp)) Pzx = eta * lamb * np.exp(-lamb * z) Pzx[z>zexp] = 0.0
Zufälliger Messwert
Zusätlich wird noch modelliert, dass der Sensor auch einfach mal etwas falsches zurück gibt, was überhaupt nichts mit der realen Welt zu tun hat. Das kann z.B. durch Quantisierungsfehler o.ä. passieren oder wenn mehrere Ultraschallsensoren an einem Roboter angebaut sind, die dann vom jeweils anderen das Echo empfangen.
\[P_{rand}(z \mid x,m) = \frac{1}{z_{max}}\]
Python Code:
Pzx = np.ones(len(z)) / maxz
Maximum Messwert Rückgabe
Das Phänomen ist im oben dargestellten Histogramm zu sehen: Es kommt gar kein Echo beim Sensor an, dadurch denkt er, der Messbereich ist völlig ausgeschöpft und gibt den maximalen Messwert zurück. In diesem Fall (Tinkerforge Ultraschall Sensor) 4m.
\[P_{max}(z \mid x,m) = \delta(z_{max})\]
Python Code:
Pzx_maxrange = np.zeros(len(zs)) Pzx_maxrange[-1:] = np.max(zs) # 400cm
Ergebnis: Zusammengesetzte Verteilung
Diese Verteilungen werden nun einfach addiert (und normalisiert).
Pzx = Pzx_hit + Pzx_unexp + Pzx_rand + Pzx_maxrange
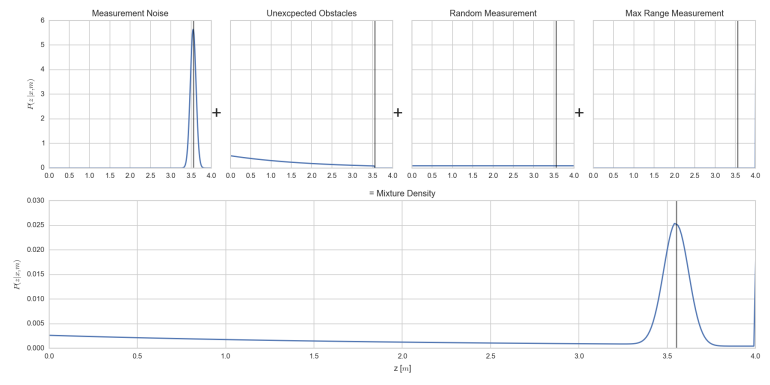
Obere Zeile: Alle 4 einzelnen Wahrscheinlichkeitsdichteverteilungen (v.l.n.r. Normalverteilung, Nicht vorhersehbare Hindernisse, Zufälliger Rückgabewert, Maximum Messwert)
Untere Zeile: Summe der 4 Verteilungen, normiert
Parametrierung
Nun ist der Anteil jeder Verteilung natürlich abhängig vom jeweiligen Sensor und Einsatzbedingung. Außerdem sind die Parameter \(\sigma_z^2\) (Varianz der Normalverteilung) und \(\lambda\) (Abflachen der Exponentialverteilung für unvorhersehbare Hindernisse) zu bestimmen. Die Wichtung der einzelnen Verteilungen wird durch die Parameter \(z\) bestimmt.
\[P(z\mid x,m) = \left(\begin{matrix}z_{hit} \\ z_{unexp} \\ z_{max} \\ z_{rand} \end{matrix}\right)^T \cdot \left(\begin{matrix}P_{hit}(z\mid x,m) \\ P_{unexp}(z \mid x,m) \\ P_{max}(z \mid x,m) \\ P_{rand}(z \mid x,m) \end{matrix}\right)\]
Die Parameter \(z_{hit}, z_{unexp}, z_{max}, z_{rand}, \sigma_z, \lambda\) sind nun geeignet zu ermitteln, damit das mathematsiche Sensormodell ideal zur Einsatzbedingung passt.
Daten, Daten, Daten
Hat man nur lange genug Realdaten gesammelt, so kann man die gemessenen Daten mit der Verteilung übereinander legen und die Parameter ‘per Hand’ anpassen, bis es augenscheinlich stimmig ist. In nachfolgender Abbildung ist zu erkennen, dass der Sensor für großen Distanzen neben dem Wahren Wert (hier: ca. 3,55m) auch maximale Messwerte und Werte vor dem Hindernis zurück gibt. Dies entspricht dem Mixture Density Model.
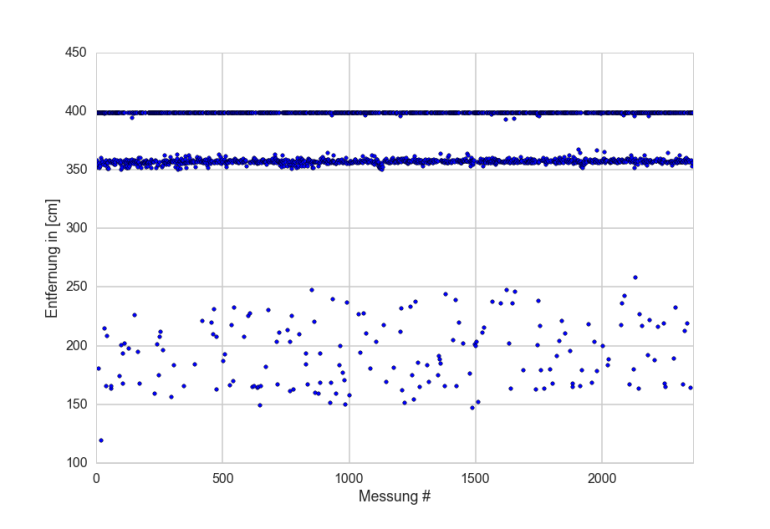
knapp 2500 Messwerte mit Tinkerforge Ultraschall-Bricklet gegen eine weiße Wand in ca. 3.55m Entfernung
Eine entsprechende ‘per Hand’ Parametrierung könnte so aussehen. Das reicht für die meisten Anwendungsfälle aus. Die benötigten Parameter sind beispielsweise:
z_hit = 7.0 z_unexp = 0.05 z_rand = 0.05 z_maxrange = 0.03 # Normalize normz = 1.0/(z_hit+z_unexp+z_rand+z_maxrange) z_hit=z_hit/normz z_unexp=z_unexp/normz z_rand=z_rand/normz z_maxrange=z_maxrange/normz def Pzx(z): # Sum of all with weighted average return z_hit*Pzx_hit(z) + \ z_unexp*Pzx_unexp(z) + \ z_rand*Pzx_rand(z) + \ z_maxrange*Pzx_maxrange(z)
Die Funktion Pzx gibt nun für jede Entfernung z die Wahrscheinlichkeit zurück, dass von dort ein Messwert zurück kommt.
Normiert ergeben sich folgende Zahlen:
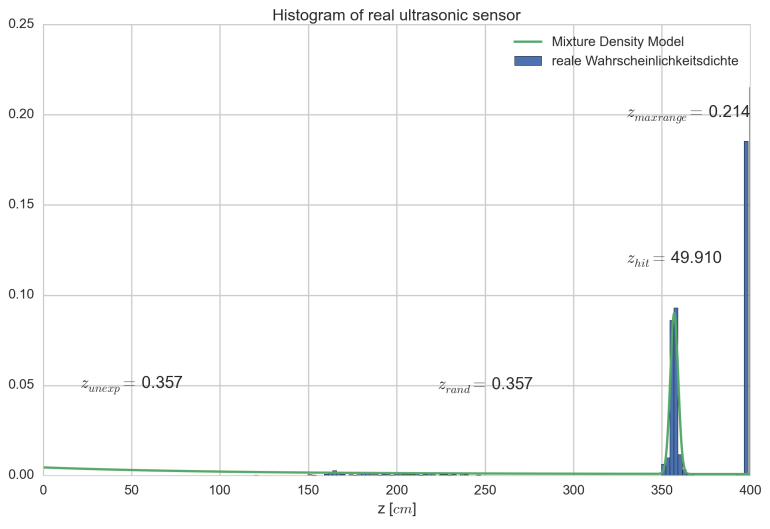
Histogram einer realen Messung (blau) und parametriertes Mixture Density Model (grün)
Das reicht für die meisten Anwendungsfälle aus. Mit dieser probalistischen Funktion kann nun von einem umherfahrenden Roboter trotz Sensorstörungen eine Karte des Raumes erstellt werden. Dieses Kapitel soll hier nicht weiter vertieft werden.
Möchte man die Parametrierung nicht per Hand machen, schlägt Thrun die Expectation Maximization vor.
Expectation Maximization
Ist das ‘per Hand’ parametrieren zu aufwendig, kann auch ein Maximum Likelihood Estimator eingesetzt werden, welcher die Parameter bestmöglich schätzt. In [Thrun, S., Burgard, W., & Fox, D. (2005). Probabilistic robotics. Retrieved from http://www.lavoisier.fr/livre/notice.asp?ouvrage=1218883] kann dieser nachgeschlagen werden.
Fazit
Ein Sensor gibt nie den Wahren Wert aus und auch nicht immer normalverteilte Messwerte um den wahren Wert. In einigen Fällen müssen noch andere Einflussparameter probalistisch berücksichtit werden, um bessere Ergebnisse zu erhalten.
In diesem Beitrag wurde gezeigt, wie die Tinkerforge Ultraschallsensoren an die gängige Literatur zur Robotik angepasst werden können. Damit sollten Robotikprojekte starten können…
