Erfasst man einen realen Vorgang mit einem Sensor, so hat man intuitiv das Gefühl, dass dieser Sensor den realen Wert ‘schon korrekt messen wird’. Das Problem ist, dass kein Sensor perfekt ist. Am Beispiel der Umfeldsensorik für PKW ist ein sehr populärer Sensor der Radar, welcher z.B. für die adaptive Geschwindigkeitsregelung ACC, Ein-/Ausparkassistenten oder auch Totwinkelassistenten eingesetzt wird.
Schaut man sich die Rohmesswerte eines solchen Sensors an, wird klar, was mit ‘nicht perfekt’ gemeint ist:
![Rohmessdaten eines Nahbereichsradarsensors für mehrere Radfahrer (blau) und KFZ (grün). Quelle: [Höringklee 2013 - Entwicklung eines Assistenzsystems zur Überwachung nicht einsehbarer Bereiche im Fahrzeugumfeld]](https://www.cbcity.de/wp-content/uploads/2013/08/Messdaten_Radarsensor_Draufsicht_Fahrrad_Kfz.png)
Rohmessdaten eines Nahbereichsradarsensors für mehrere Radfahrer (blau) und Fahrzeuge (grün), welche sich an den Sensor (schwarzes Kreuz links) annähern. Quelle: [Höringklee 2013 – Entwicklung eines Assistenzsystems zur Überwachung nicht einsehbarer Bereiche im Fahrzeugumfeld]
Ist dort etwas?
Kommt dort etwas?
Wie schnell ist es?
Was ist es?
Rohmessdaten als Futter für Algorithmen
Die Rohmessdaten des Sensors gehen immer durch einen Algorithmus, welcher entscheiden muss, was dort ‘zu sehen’ ist.
Oftmals ist ein Sensor auch nicht ausreichend, um die Entscheidung vollständig und sicher treffen zu können. Daher wird oft Radar+Video fusioniert oder auch Stereovideo+Radar oder Video+Lidar oder oder oder.
![Visualisierung von Rohmessdaten eines Radarsensors während der Vorbeifahrt eines Objekts (Fahrzeug oder Fahrrad) am Sensor. Quelle: [Höringklee 2013, wie oben]](https://www.cbcity.de/wp-content/uploads/2013/08/Object-passing-Radar.gif)
Visualisierung von Rohmessdaten eines Radarsensors während der Vorbeifahrt eines Objekts (Fahrzeug oder Fahrrad) am Sensor. Quelle: [Höringklee 2013, wie oben]
Algorithmen verstehen nur Zahlen
Das Problem an der Sache ist, dass ein Mikrocontroller (Steuergerät), ein PC, allgemein ein Algorithmus, nur Zahlen versteht. Wir als Menschen schauen das Fahrrad an und sagen: Klar, ein Fahrrad, welches auf uns zu kommt, ich kann jetzt nicht auf die Straße laufen. Doch wie soll ein Mikrocontroller das verstehen?
Die Lösung: Man muss ihm als Funktionsentwickler einen strukturierten, wiederholbaren, eindeutigen Ablauf geben, wonach er die Rohmessdaten klassifizieren kann.
Ein sehr einfaches Beispiel wäre, wenn man aus zwei hintereinander gemessenen Positionsinformationen eines Objekts die Fahrtrichtung und die Geschwindigkeit bestimmt. Dies geht mathematisch mit dem Pythagoras und der Annahme einer konstanten Geschwindigkeit:
Diese Informationen können nun genutzt werden um Entscheidungen zu treffen. Geht man beispielsweise davon aus, dass man die Rohmesswerte eines Radarsensors alle 20ms über den CAN-Bus übermittelt bekommt, so hat man eine Messung für x und y (also die Position) alle 20ms neu. Man kann in einer Sekunde
Messwerte erhalten. Geht man weiterhin davon aus, dass ein PKW, welcher sich dem Sensor nähert, seine Bewegung in dieser kurzen Zeit kaum verändern kann, also die gemessene Richtung φ und auch die Geschwindigkeit v nahezu den gleichen Wert haben müssten, so kann man eine Modellschätzung vornehmen.
Parameter schätzen
Geht man davon aus, dass der Sensor stochastisch falsch misst, also der gemessene Wert mit einer Normalverteilung um den wahren Wert streut, so kann man auf eine Vielzahl von Schätzverfahren zurückgreifen, um einen Anhaltspunkt über die gemessene Größe zu erhalten. Ein sehr sehr einfacher Schätzer ist der Maximum Likelihood Schätzer, welcher einen unbekannten, konstanten Parameter aus verrauschten Messwerten ermittelt.
Maximum Likelihood Schätzer (ML)
Der geschätzte Wert, z.B. die Richtung φ in die das Fahrzeug unterwegs ist, kann durch Maximierung der Likelihood Funktion über die Messwerte Z ermittelt werden.
Einfach formuliert: Welcher Parameter φ erklärt die Messung Z am besten?
Nimmt man an, dass die Messwerte für φ normalverteilt um den realen Wert liegen, so kann man jeden Messwert gegen eine Normalverteilung testen und schauen, wie gut dieser Messwert zu der Verteilung passt.
Die Implementierung des Maximum Likelihood Schätzers in Matlab ist nachfolgend:
s=2; % angenommene Standardabweichung der Messwerte
range=40:0.1:60; % Testwerte für Fahrrichtung
for i=1:length(range)
% Likelihoods berechnen
L(i) = sum(1/sqrt(2*pi*s^2)*exp(-(phi-range(i)).^2/(2*s^2)));
end
[maxL,index]=max(L); % Parameter mit Maximum Likelihood
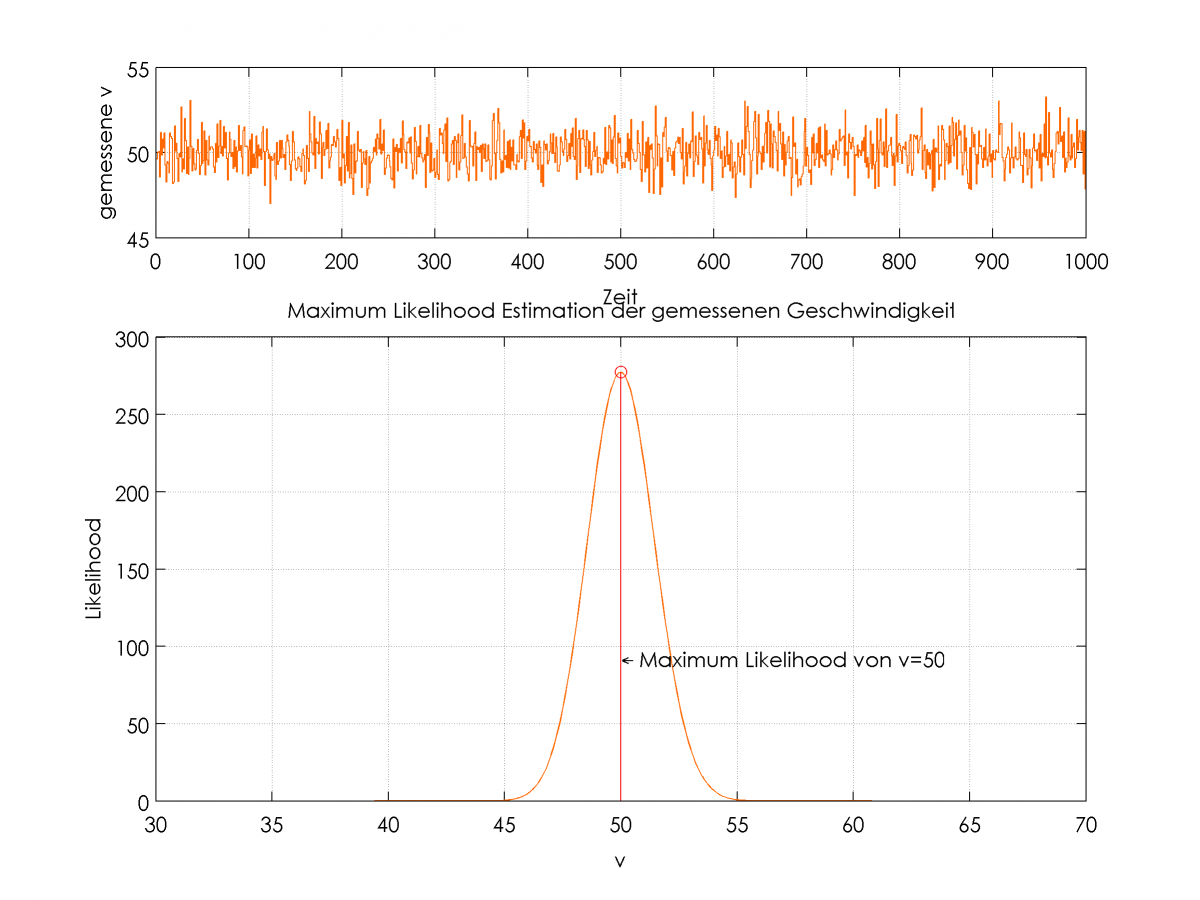
Die geschätzte Verteilung ergibt sich dann beispielsweise wie in folgender Abbildung:

Eintreffende Messwerte (oben) und Entwicklung der Likelihood-Funktion für die Schätzung
Es ist deutlich zu erkennen, dass die Funktion bei φ=50° ein Maximum hat, welches die gemessenen Werte am besten repräsentiert. Der Schätzer ist asymptotisch erwartungstreu und effizient, was bedeutet, dass er mit minimalstem Fehler den realen Wert ermittelt, obwohl die Messwerte offensichtlich verrauscht sind.
Die Standardabweichung der Normalverteilung wird dabei mit jedem eintreffenden Wert geringer, der Mittelwert nähert sich dem realen Wert an.
Mit fahrzeugtypischen Zykluszeiten von 20ms entspricht die animierte Abfolge ca. 1s im Fahrzeug. Eine sehr lange Zeit, wenn man bedenkt, dass ein Fahrzeug mit 50km/h in dieser Zeit ca. 14m zurücklegt. Es muss also ein Schwellwert definiert werden, ab dem der Algorithmus entscheidet: OK, da ist wirklich etwas und es nähert sich mit ?km/h.
Entscheidungsschwelle
Am Beispiel des MLE kann man sich als Entscheidungsschwelle die Varianz des Messwerts herausgreifen. Diese ist das Quadrat der Standardabweichung, welche im MLE ohnehin zyklisch ermittelt wird. Eine iterative Variante , welche einen sehr geringen Implementierungsaufwand bedeutet, ist die gleitende Mittelwert- und Varianzberechnung:
var_ml(k) = var(messwert(1:k)); % Varianz der Schätzung
Dabei bezeichnet k den aktuellen Messwert.
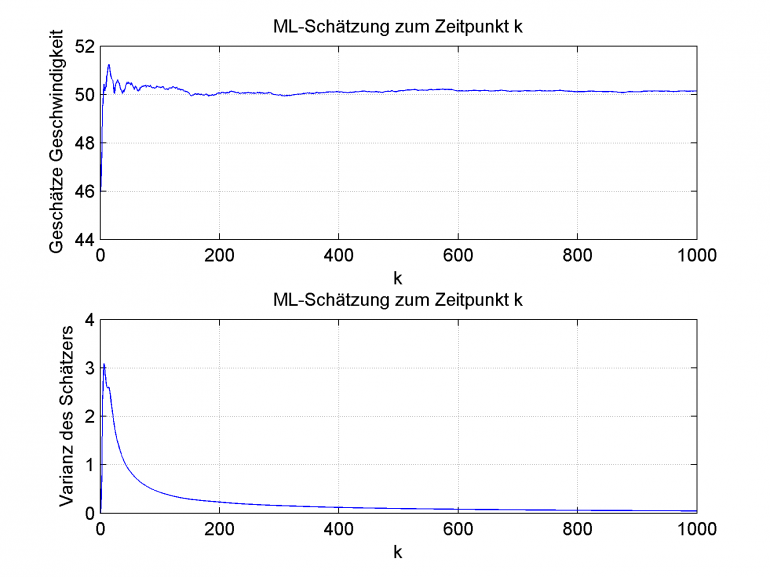
Mittelwert einer ermittelten Geschwindigkeit (oben) und Varianz dieses Wertes (unten)
Es ist deutlich zu erkennen, dass bei einem konstanten Schätzwert, was ja Voraussetzung für den MLE war, die Varianz der Schätzung mit zunehmender Zykluszahl gegen einen Wert konvergiert, welcher Abhängig vom Sensorrauschen ist.
Die Aufgabe des Applikationsingenieurs ist es nun die Grenzwerte und Parameter so zu bestimmen, dass der Algorithmus mit einer sehr hohen Wahrscheinlichkeit alle Objekte erkennt und diese auch richtig parametriert.
Denn dies war alles nur der Vorverarbeitungsschritt, denn die Informationen, dass ein Objekt an einem Ort mit einer Geschwindigkeit ist und in eine Richtung fährt sind ja erst die Eingangsparameter für Zustandsschätzer.