OK, jeder Ingenieur hat nach der Ankündigung “Timo Boll gegen KUKA Roboter” und dem imposanten Teaser Video wahrscheinlich ein lächeln im Gesicht gehabt. KUKA, das deutsche mittelständische Unternehmen einen YouTube Hit? Richtig gutes Marketing? Wow, das kann was werden.
Doch dann die Ernüchterung: Das angekündigte Match war doch nur ein “Werbespot“. Doch wieso eigentlich?
Das Problem am Tischtennis spielen gegen einen Roboter ist eigentlich nicht die Roboterbewegung sondern etwas ganz anderes.
Wo ist der Ball?
Möchte man gegen einen Menschen Tischtennis spielen, muss man erst mal heraus bekommen, wo der Tischtennisball eigentlich ist. Den Ball muss man optisch verfolgen, d.h. man benötigt High-Speed Videokameras oder im Ball eine LED und Infrarotkameras. In folgendem Video sieht man die OpenCV (Open Computer Vision) Bibliothek, welche den Job richtig gut macht (das Video hat kein Audio):
Man erkennt auch, dass durch die schnelle Bewegung des Balls das Ergebnis nicht immer eindeutig ist, die Pixel der Kamera ohnehin nur eine endliche Auflösung zulassen.
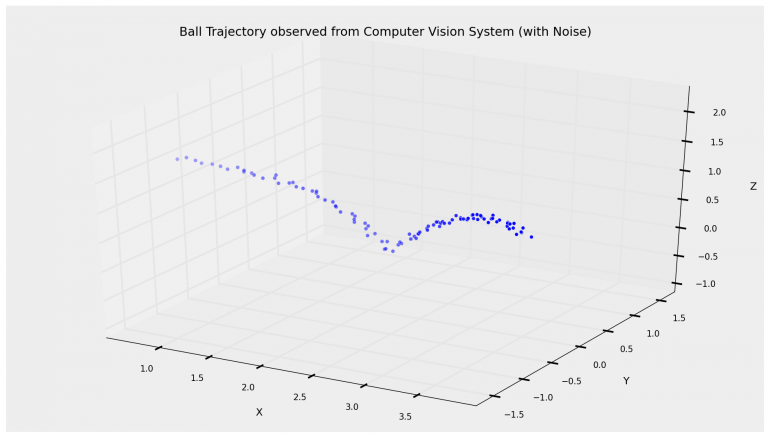
Das Ergebnis der Objekterkennung muss also definitiv noch durch einen Filter.
Kalman Filter zur Objektverfolgung
Das Standardverfahren zur Objektverfolgung bei “verrauschten” Messgrößen ist das Kalman Filter, welches 1960 von Rudolf Emil Kalman entwickelt wurde und dann auch gleich bei der Mondlandung half.
Das Filter kann mit verschiedenen Dynamiken aufgesetzt werden. Für einen Ball, der sich prinzipiell in alle Richtungen bewegen kann, wird typischer Weise eine Filterdynamik angesetzt, welche von einer Objektbewegung mit konstanter Beschleunigung ausgeht.
Die Systemdynamik eines “Konstant-Beschleunigungs-Modells” in 3D ist:
\(x_{k+1} = \begin{bmatrix}1 & 0 & 0 & \Delta t & 0 & 0 & \frac{1}{2}\Delta t^2 & 0 & 0 \\ 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & \frac{1}{2}\Delta t^2 & 0 \\ 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & \frac{1}{2}\Delta t^2 \\ 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ \dot x \\ \dot y \\ \dot z \\ \ddot x \\ \ddot y \\ \ddot z\end{bmatrix}_{k}\)Damit kann nun modelliert werden, dass ein Objekt mit konstanter Beschleunigung durch den Raum fliegt. Perfekt also für einen Tischtennisball.
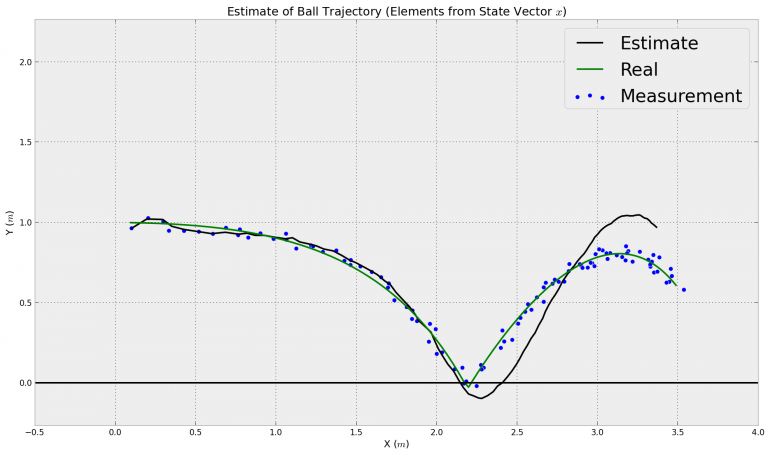
Geschätzte Trajektorie des Ball durch Kalman Filter
Wie man an der Abbildung sieht, funktioniert die Positionsschätzung des Balls trotz verrauschter Positionsmessungen sehr gut, damit wüsste der KUKA definitiv, wohin er sich bewegen soll. Doch was dann?!
Sobald der Ball aufsetzt, ist das Filter völlig verwirrt und schätzt die Position nicht mehr richtig.
Nichtlineare Bewegung des Balls
Genau genommen ist sogar der Luftwiderstand des Balls schon nichtlinear (weil quadratisch von der Geschwindigkeit abhängig), kann aber durch das Filter noch relativ problemlos kompensiert werden. Das Aufsetzen auf der Tischtennisplatte ist allerdings eine starke Verletzung des linearen Systemverhaltens, denn plötzlich ändert sich die Geschwindigkeit (in Y-Richtung) praktisch mit Vorzeichenwechsel. Damit kommt das Filter nicht klar.
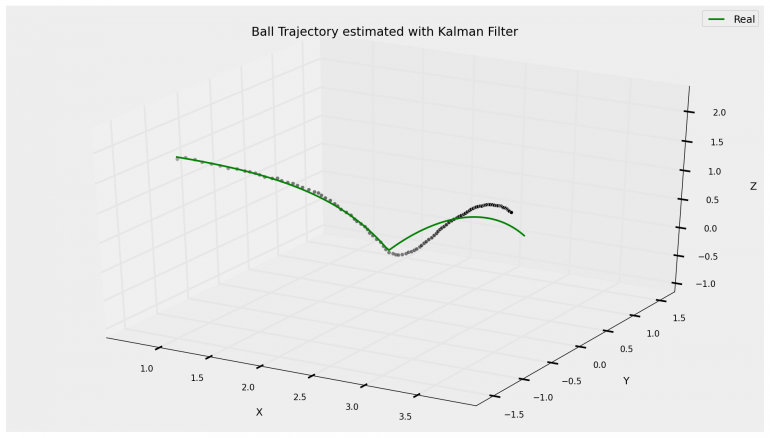
Natürlich kann man nun prinzipiell einen Extended Kalman Filter ansetzen, welcher mit nichtlinearen Systemdynamiken klar kommt, allerdings bleibt dann immer noch ein großes Problem:
Timo Boll kann machen, dass der Ball beim Aufsetzen in eine andere Richtung springt. Ein Mensch als Gegenspieler kann beobachten, wie Timo Boll die Kelle führt und daraus ableiten, wie der Drall des Balls ist und wohin er springen wird nach dem Aufsetzen (oder schon in der Luft). Das müsste das Computer-Vision System ebenfalls können, um wirklich eine Chance gegen einen guten Spieler haben zu können. Alternativ kann das Tracking erst nach dem Aufsetzen des Balls beginnen. Ob dann die Zeit zum Bewegen des Roboterarms noch reicht?!
Einen wirklichen Marketing-Buzz kann jetzt die Firma ernten, die das Tracking System für KUKA hat, denn ich denke daran ist die Idee des realen Matchs auf Augenhöhe gegen Boll gescheitert.
Der wahre Gewinner des KUKA Marketing Flops
Ganz klar: Ulf Hoffmann. Er hat die Idee auch gehabt und in seiner Garage nachgebaut und wirklich gezeigt, dass sein Roboter es kann. Zumindest für geradliniges Zuspiel.
[Update 14.03.14] Armin Hornung (vom Robot Lab der Uni Freiburg), weist auf ein paar Ungereimtheiten im Video von Ulf Hoffmann hin:

Der Roboterarm verschwindet irgendwie

Die Videokamera in der Ecke ist durch die Kelle sichtbar
Wieso, warum, weshalb?! Keine Ahnung.
Die komplette Implementierung des Kalman Filter zum Tracking eines Balls, implementiert in Python ist hier zu finden.
Disclaimer: Ich habe die Implementierung testweise gemacht, sie erhebt keinen Anspruch auf “Stand der Technik”. Vielmehr stellt sie einen simplen Standardfall dar, welcher mir von jedem Computer-Vision Experten um die Ohren gehauen werden kann. Ich bitte um entsprechendes Kommentar. :)






2 Comments
Der im Artikel gemachte Fehler ist eine Annahme einer sturen Berechnung nach Ablauf.
Wenn ein Mensch ähnlich Tischtennis spielen würde, dann würde er ebenfalls keinen Ball erwischen (wie schnell ist eigentlich das Auge?).
Was man aber wunderschön berechnen kann:
Vorraussagen wo der Ball auftreffen wird.
Und dann wirds interessant. Dann kann man nämlich aufgrund der vorherigen Werte (Geschwindigkeit usw) aus 2 Vektoren einen “Trichter” bilden und vorraussagen, wo sich der Ball wahrscheinlich befinden wird. Da man das sogar noch vor dem Aufsetzen tun kann, braucht man dann a) nur einen geringeren Auschnitt des Bildes auf einen Ball zu überprüfen (spart Rechenzeit), weiß b) wo sich der Ball auf der Z-Achse befinden wird und kann c) den Aktor schonmal in die richtige Richtung fahren. Selbst einen gewissen Anschnitt des Balles kann man damit kompensieren.
Ähnlich wie ein Mensch, der schließt auch aus Erfahrungen wo der Ball ungefähr sein wird.
Eine Anwendung von solchen Abschätzungen unter Extrembedingungen ist übrigens Iron Dome (oder andere Raketenabwehrtechnik): dort wird vermutet, wo die Rakete wann sein wird und die Abwehrwaffe direkt zum Rendevouzpunkt geführt (nicht nachgeführt), wo dann nur noch Feinkorrekturen vorgenommen werden bzw eine eigene Suche aufschaltet.
Interessante Ergänzung. Danke!